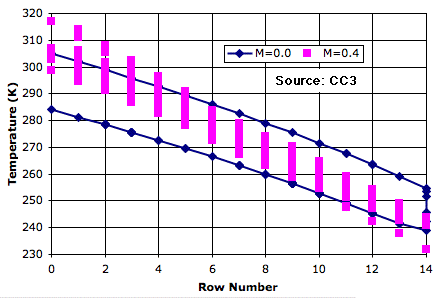
In any given row of the atmosphere, the cell is 20 K warmer on the way up than on the way down. Even though a rising cell may pass by a falling cell, they exchange no heat. The convection is adiabatic. The average temperature of the bottom row is roughly 50 K warmer than the average temperature of the top row.
Now suppose we allow the passing cells to exchange heat. The warm, rising cells cool down because they mix with the cool, falling cells. In order to reach the top, a cell will have to start off hotter than it would without mixing. Cells rise part-way, mix with their neighbors, fall, and mix with their neighbors again. The pink plot shows the variation in temperature, with mixing fraction 0.4, as a cell rises and falls during a hundred thousand iterations of the simulation. The average temperature of the bottom row is roughly 70 K warmer than the top row.
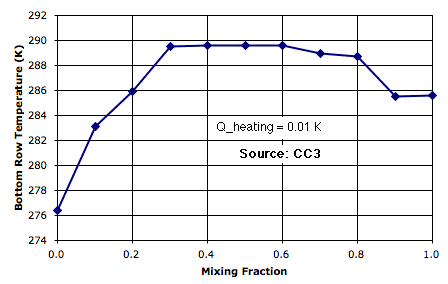
The following plot shows how bottom-row temperature varies with mixing fraction for Q_heating at 0.01 K. (Thanks to Peter Newnam for the data.) As we increase the mixing, circulation is further impeded, but but the mixing itself begins to transport sufficient heat to bring down the surface temperature.
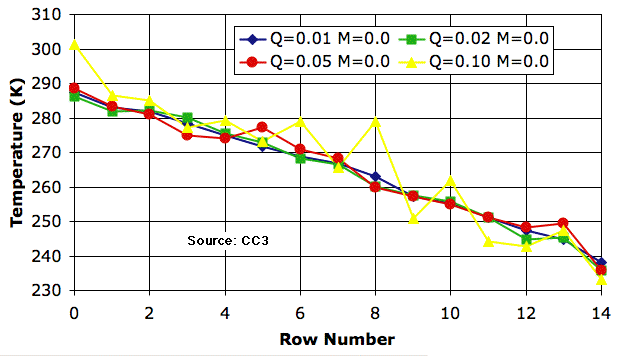
Circulation alone is an efficient transporter of heat. The following plot shows that we see little change in the atmospheric temperature profile as we increase Q_heating by a factor of ten from 0.01 K to 0.1 K. The profile for 0.1 K is erratic, but on average is almost the same as that for 0.01 K.
When we allow mixing, we break up the continuous circulation that would otherwise transport heat from the surface to the tropopause. Instead of one continuous circulation we have a series of circulations carrying heat up in stages. Heat transport between stages takes place by mixing. The average temperature of the surface must increase because heat exchange by mixing requires an additional temperature drop over and above the adiabatic temperature drop produced by circulation.
To round off our explanation of the effect of mixing, imagine a continuous circulation from bottom to top consisting of two parallel columns of cells. One column is rising as the other falls. Now we suppose that each rising cell must be 10 K warmer than its side-by-side neighbor in the falling column, or else circulation will stop. Furthermore, we suppose that each time the circuit rotates by one cell, we allow some mixing between the side-by-side neighbors. The rising cell cools by 1 K and the falling cell warms by 1 K. Because of this mixing, a cell that has just descended will be 1 K warmer than without mixing. If it is to be 10 K cooler than its new side-by-side neighbor, this neighbor must be 1 K warmer than in circulation without mixing. The 10-K difference between the side-by-side neighbors in the column will be sustained only if the total temperature drop from bottom to top increases by 1 K multiplied by the number of cells from bottom to top. In our case, that would be 15 K.
Mixing raises the temperature difference necessary to transport heat through the atmosphere. The temperature difference is therefore greater than that dictated by adiabatic convection alone. In future posts we will enhance our simulation to allow cells within the array to radiate heat directly into space. This radiation, taking place before the cells reach the tropopause, will decrease the temperature drop between the bottom and the top. For now, however, we are satisfied that our program is effective in its simulation of mixing and circulation.

We tracked the temperature of individual cells by marking a cell and inserting the following code in the swap_cells routine. The result is the row number and temperature every time the cell moves. We get a lot of lines in the reporting window.
ReplyDeleteif {[winfo exists .reporting.text]} {
set line ""
global array_width
set c [lindex $cells [expr $j1 * $array_width + $i1]]
scan $c %d%d%f%s%s j i T name type
if {$type == "marked"} {
.reporting.text insert end "$j [format %.1f $T]\n"
}
set c [lindex $cells [expr $j2 * $array_width + $i2]]
scan $c %d%d%f%s%s j i T name type
if {$type == "marked"} {
.reporting.text insert end "$j [format %.1f $T]\n"
}
}
Kevan,
ReplyDeleteI think that the steady state of the column of air requires that the basic hypotheses of the analysis are established at the end. In our case you assume that the base of the column is heated to a constant rate Qh (K/step) while its summit is cooled to the floating rate Qh*(Ttop/250)^4 (K/step). Thus, at the end (to the equilibrium), the mean Ttop will have to be equal to 250 K. But Ttop is always lower than 250 K, the simulation doesn't converge and it stops when the column would still be warming up.
Why? Does the simulation affect this behavior? How? Answering this questions seems to me the fundamental priority.
Michele
Dear Michele,
ReplyDeleteIf you turn off the circulation and set the mixing fraction to some value between 0.1 and 1.0, you will see that the top layer does indeed converge to 250 K. When we turn off the mixing, and allow only adiabatic circulation, the average temperature of the top row falls to 240 K. At first I thought this was because the effective radiating temperature, being the fourth root of the mean fourth power of the top row cell temperatures, was equal to 250 K, while the average (the first root of the mean first power) was only 240 K. But further investigation shows that the effective radiating temperature is around 240 K also.
The top layer will cool at a rate of 0.01 K/iteration if it is at 250 K. The bottom layer warms by 0.01 K/iteration always. My implementation of adiabatic expansion must be slightly wrong, so that the top layer has to cool only at 0.0085 K/iteration in order to get rid of the heat coming in at the bottom.
I could easily be introducing such a problem with rounding errors. I'll look into it.
Yours, Kevan
Dear Michele,
ReplyDeleteI think I know what it the problem is. Hot air expanding from p1 to p2 does more work than it takes to compress cold air from p2 to p1. I describe this phenomenon in Work by Convection.
http://homeclimateanalysis.blogspot.com/2010/04/work-by-convection.html
Our block of four cells rotates when doing so will drop its center of gravity. A warm cell rises. A cold cell falls. We calculate their final temperatures using the equation for adiabatic expansion and compression. But we have ignored the excess work done by the rising cell. It just disappears in our current simulation.
I propose that by the time a cell gets to the top, the we have 0.0015 J of heat vanishing for every 0.01 J that we put in at the bottom. Thus it has only 0.0085 J remaining to radiate, which drops the top layer temperature from 250 K to 240 K.
I'll have to check the numbers tomorrow. Now the question arises: what shall we do with this missing heat, which is work that will be done on the bodies of air? This work provides the power for weather. Shall we turn it directly into heat, assuming viscous action within the block? Or do we need to turn it into some other phenomenon that is larger than a block of four cells?
Yours, Kevan
Kevan,
ReplyDeleteThe vanishing heat is 15% of that you put in at bottom. It’s far great and occurs with circulating ad mixing and hence it can’t be affected by anything you don’t introduce with some procedure.
I think the answer is into the simulation.
Michele
Actually: the heat does not vanish when we turn off the circulation. With mixing alone, the top row reaches 250 K. Try running with mixing_fraction 1.0 and Q_heating 0.01 and you will see what I mean. It's the circulation that makes the heat disappear.
ReplyDeleteWhen the circulation routine rotates four cells, it always decreases the total internal energy of the four cells. On average, the sum of the temperature of the four cells decreases by 0.06 K.
So I have modified the circulation routine for CC4. It calculates the work done as the loss of total temperature, and adds it back to the cells uniformly (one quarter to each). That is: we assume the work is dissipated locally as viscous friction.
I run with no mixing and after 500,000 iterations, the top row has an effective radiating temperature of 250 K and an average temperature of 245 K.
When I turn on the mixing with mixing fraction 0.1 the surface warms up by around 20 K. I'll have to re-plot some graphs.
So I think the program converges properly, and our previous conclusions about mixing remain intact.
Yours, Kevan
CORRECTION: With circulation only, the top row average temperature converges to around 249 K while effective radiating temperature is around 250 K. The standard deviation of the top cell temperature is 4 K. Kevan
ReplyDeleteI ran the simulation with mixing 0.1, and 0.4. The mixing still warms up the surface by 10 K and 20 K respectively. I'll dedicate the next post to this topic. Thanks for your advice. Kevan
ReplyDeleteKevan,
ReplyDeleteI ran CC_3 with MR = 0.1 obtaining Tb – Tt = 835 – 250 = 585 K and with MR = 1.0 obtaining Tb – Tt = 309 – 250 = 59 K. There is MR(Tb – Tt) = constant bearing out that your mixing is in practice the thermal conductivity.
I think that is wrong to introduce the viscosity in explaining what occurs without it. Your circulating proc is simply incomplete because you don’t take into account that the cell in rising/falling expands/(is compressed) adiabatically and simultaneously varies its gravitational potential energy. When the cell pass from the row j to the row j+1, its potential energy increases of g*5000/15 (J/kg) and this amount is yielded by the enthalpies of the cell. So the temperature decreases of (g/Cp)*5000/15 = 10/3 K.
Of course the opposite occurs in falling where the temperature increases of 10/3 K.
Michele
Dear Michele,
ReplyDeleteThank you for your test of the mixing.
I don't think I understand what you are saying about the gravitational potential energy. My cell mixing routine neglected the work available from convection. The work disappeared. That's unrealistic. The work available goes into moving the cells by pushing outwards. So in CC4 I calculate the work available and I assume that it is dissipated as viscous heat within the cell.
When we rotate a cell, its center of mass drops. When the cells below a block heat up, its center of mass rises. We ignore the effect of gravitational potential, except in its effect on pressure.
A steel ball we lift 100 m up may gain potential energy, but in Thermodynamics it undergoes no change in its properties. The gravitational potential term is added to the enthalpy equation in order to allow enthalpy to be conserved in a gravitational field. Potential energy is a mathematical construction, not an observable property.
When one cell in our system loses potential energy, this means that another cell must gain energy of some sort. As we heat up our entire array, it does gain potential energy because it expands. We are ignoring this effect.
But I don't see how gravitational potential energy can affect the properties of the cells in a circulation.
Yours, Kevan
I intend to say that the four cells of the group compose a thermodynamic system where they change the spatial position in compliance with the law of conservation of energy stating Qe + We = ΔE where Qe is the heat exchanged by the cells with the surroundings (>0 when it is yielded to the cells), We is the work exchanged by the cells with the surroundings (>0 when it is done on the surroundings) and ΔE is the resulting range of the total energy of the group of cells, constituted by the total thermodynamic energy CpΔT (the enthalpies and so there isn’t the need to compute the thermodynamic works), potential gravitational energy gz, macroscopic kinetic energy u²/2, viscosity losses, etc.
ReplyDeleteIn our case, for the four cell of the group, is ΔE = M•Σ(CpTj + gzj) = 0 as Qe = We = 0.
M, Tj and zj are respectively the mass, the temperature and the height of center mass of each cell.
The circulating routine rotate the cells until the center mass of the four cells becomes the lowest without turn the drop of potential energy M•Δ[Σ(gzj)] into the correspondent increase of enthalpies and so the group of four cell loses the said amount M•Δ[Σ(gzj)] at each iteration.
There is no vanishing energy, it is the routine that throws away a bit of energy per
iteration.
I noticed you assume that the lower edge of the two lower cells are at the same altitude and the height of the cell is its temperature. Then, the sum of the temperatures (the total height) of the cells below the two lower cells would be the same. What issues would arise by this approximation?
I have a doubt. A cell has the volume V = MRT/p = hA and then, being the cross section of the columns the same, the height of the cell would be h = T/p (missing the constants). Perhaps, is my understanding wrong?
Keep well.
Michele
Kevan
ReplyDeleteI have modified your proc swap_cells as follows
global cells p_step_fraction R_air Cp_air cell_accelerate p_bottom p_top p_step
set T1 [get_temp $j1 $i1]
set T2 [get_temp $j2 $i2]
set p1 [expr $p_bottom*(1.0-$p_step_fraction*($j1-0.5))]
set p2 [expr $p_bottom*(1.0-$p_step_fraction*($j2-0.5))]
set delta_T [expr 0.5*$p_step*$R_air/$Cp_air*($T2/$p2+$T1/$p1)]
set_temp $j1 $i1 [expr $T2 + ($j2-$j1)*$delta_T]
set_temp $j2 $i2 [expr $T1 - ($j2-$j1)*$delta_T]
set O1 [get_type $j1 $i1]
imposing the total energy conservation CpΔT + gΔz = 0 and hence ΔT = -gΔz/Cp.
With MR = 0, T_bottom tends to 300 and T_top to 250
With MR = 0.1, T_bottom tends to 310 and T_top to 250
With MR = 1, T_bottom tends to 310 and T_top to 250
We know that T_bottom would be T_top*(p_bottom/p_top)^(R/Cp) = 250*2^(1/3.5) = 305 K. The error of simulation is only ±1.6% and that is very satisfying.
Michele
Dear Michele,
ReplyDeleteThanks for your latest contributions. I agree that it was the simulation that threw away energy every time it rotated the cells. I agree that the height of a cell is h = T/p, and my own circulation routine accounts for this when determining the altitude of the center of mass after rotation.
I see that in your swap routine you give cells a half-step of pressure. I don't do that. It may be that I should, in order to improve the accuracy of the convergence.
I think our two explanations of what is going on are equivalent. Once again, I like the way you use gravitational potential energy to simplify the calculations.
A rising cell of warm air does a certain work Wr when it expands from p1 to p2 (p2 < p1). A falling cell of cold air requires a certain work Wf to compress from p2 to p1. We rotate cells when there will be a net drop in the center of mass. Because of the ideal gas law, the center of mass drops if and only if Wf < Wr.
On average, Wf is slightly less than Wr. We find that the total temperature of our gas drops by 0.06 K on average, which is 0.015 K/kg, which is roughly 15 J of heat. so Wr−Wf = 15 J.
Until now, our simulation ignored this 15 J. But it will go into stirring up the gas, and I now add the 15 J back in evenly to all four cells, and say it's viscous heat.
When you say CpΔT + gΔz = 0 and hence ΔT = -gΔz/Cp you are ignoring the rotational kinetic energy of the circulating gas, which amounts to 15 J. But let's suppose we allow the circulation to come to a stop by viscous action. In that case your formula must apply again. Suppose the surface below the gases is rigid, so we can do no work upon when the center of mass of the gas falls down. Then We=0, as you say. All our 15 J ends up as heat in the gas, and looking from outside there is a drop of the center of mass.
Thus we find that the excess work Wr>Wf is equal to the loss of gravitational potential energy of the block.
I will post soon the new CC4, which eliminates the swap_cells routine and does the entire circulation in the circulate routine.
Yours, Kevan
Dear Michele,
ReplyDeleteMy above comment is not correct. The adiabatic work and the gravitational work are not the same.
Looking from the outside of a block of cells, we see the center of mass drop when we rotate. Because we assume Cp is constant, we must have an increase in the sum of the temperatures of the cells after the rotation.
But when we heat up the cells, we ignore the fact that the heat we put in causes the center of mass of the cell to rise. The temperature of the cell will be lower than our simple T = Q/Cp calculation suggests. Some of the heat turns into work, and raises the cell.
A 300 kg/m2 column of air at 300 K will be roughly 250 m high. At 320 K, after heating, it will be 267 m high. The center of mass will move by roughly 8.5 m, so we have 8.5 m * 10 m/s/s * 300 kg = 26 kJ of gravitational potential. (I posted this comment with the wrong math here, deleted the comment, and re-posted.) To raise the temperature of the gas by 20 K we need to put in 20 * Cp * 300 kg + 26kJ = 6.026 MJ of heat. Or we could say that 6 MJ of heat does not raise the temperature by 20 K, but by only 19.91 K.
In CC3, we ignore the increase in gravitational potential when the gas is heated. We ignore the effect when the blocks rotate. We ignore the effect when the cells cool. We could account for gravitational potential by adjusting the heating routine, the rotation routine, and the cooling routine. But we cannot adjust the rotation routine alone.
In CC3 we also ignore the work available from the rotation, which is independent of the gravitational work. In this case, we can correct the problem by adjusting the rotation routine alone. In CC4 I have taken this additional work and added it back into the block so as to represent viscous dissipation of the movement of gas caused by the excess work.
Yours, Kevan
“half-step of pressure”
ReplyDeleteThe pressure of the cell varies with z and, as we use a constant its value for teh whole cell, I think is more exact to refer to its mean value at the center of the cell.
“rotational kinetic energy of the circulating gas, which amounts to 15 J”
In this case I refer to the gas at rest, if I can say, I am doing a “thermostatic” rather than a “thermodynamic” talking. The velocities and the dissipations are missing.
One kg of gas holds pv = RT (J/kg) of thermo-elastic energy and CvT (J/kg) of microscopic kinetic (thermal) energy and its total thermodynamic energy is h = CvT + pv, i.e. the enthalpies.
If the gas changes state, its elastic energy varies as d(pv) = pdv + vdp and there occurs both the external work of expansion (pdv), used in displacing the surrounding gas (equal to –CvT if the change of state is adiabatic), and the internal work (vdp) stored into the gas as elastic energy. In other words if we displace a body using a spring, we must do both the work in displacing the body, and the one in compressing the spring. So, the total needed work is computed more easily as Δh = CpΔT, rather than as int(pdv) + int(vdp).
Indeed, the vanishing energy is the internal work int(vdp) = int(Adp/p^(Cv/Cp)) = (Cp/R)[(p2v2)^(Cp/Cv) - (p1v1)^(Cp/Cv))], if I am not mistaken. The missing 15J are the no computed internal work.
Michele
Michele: In your version of swap_cells, you warm up a falling cell by the same absolute temperature that you cool down a rising cell. In fact, you should multiply the rising temperature by T_step < 1.0 and divide the falling temperature by T_step. By this means you can get a net loss of temperature, which is where the work of rotation comes from. Kevan
ReplyDeleteDear Michele,
ReplyDeleteI forgot to say: I am impressed at how fast you learned Tcl.
Here is a table of p_factor and T_factor, where p_factor is the factor by which we multiply pressure in row j to get pressure in row j+1, and T_factor is the same for temperature assuming adiabatic expansion from row j to j+1.
j p_factor T_factor
0 0.9667 0.9903
1 0.9655 0.9900
2 0.9643 0.9896
3 0.9630 0.9893
4 0.9615 0.9888
5 0.9600 0.9884
6 0.9583 0.9879
7 0.9565 0.9874
8 0.9545 0.9868
9 0.9524 0.9861
10 0.9500 0.9854
11 0.9474 0.9846
12 0.9444 0.9838
13 0.9412 0.9828
If we have a cell at 320 K in row j=0 and another at 300 K in row j=1, we can see that if we exchange them, we get a new cell in j=1 with temperature 316.89 K. The other cell becomes a new one in j=0 with temperature 302.93 K. The first one cooled down by 3.11 K while the other one warmed up by 2.93 K.
We are missing 0.18 K * 1000 J/kgK = 180 J/kg of the work done by the expanding cell. This is the work that accelerates the gases and, I claim, we can simulate as viscous friction in the block of four cells.
Yours, Kevan
“half-step of pressure”
ReplyDeleteThe pressure of the cell varies with z and, as we use a constant its value for the whole cell, I think is more exact to refer to its mean value at the center of the cell which are hundred meters high.
“rotational kinetic energy of the circulating gas, which amounts to 15 J”
In this case I refer to the gas at rest, if I can say, I am doing a “thermostatic” rather than a “thermodynamic” talking. The velocities and the dissipations are missing.
One kg of gas holds pv = RT (J/kg) of thermo-elastic energy and CvT (J/kg) of microscopic kinetic (thermal) energy and its total thermodynamic energy is h = CvT + pv, i.e. the enthalpies.
If the gas changes state, its elastic energy varies as d(pv) = pdv + vdp and there occurs both the external work of expansion (pdv), used in displacing the surrounding gas (equal to –CvT if the change of state is adiabatic), and the internal work (vdp) stored into the gas as elastic energy. In other words if we displace a body using a spring, we must do both the work in displacing the body, and the one in compressing the spring. So, the total needed work is computed more easily as Δh = CpΔT, rather than as int(pdv) + int(vdp).
Indeed, the vanishing energy is the internal work int(vdp) = int(Adp/p^(Cv/Cp)) = (Cp/R)[(p2v2)^(Cp/Cv) - (p1v1)^(Cp/Cv))], if I am not mistaken. The missing 15J are the no computed internal work.
I agree whit you, My compute is approximate but the error is about 1.6%.
Michele
PS: it's the third time that I try to post this comment.
I modified your "Planetary Greenhouse" as follows
ReplyDeletefor …
set_temp 0 $i [expr [get_temp 0 $i] + $Q_heating * $heating_interval]
set T_top [get_temp $j_max $i]
set_temp $j_max $i [expr $T_top - $Q_heating * $heating_interval]
if …
So we have only the condition Q_bottom = Q_top. Here are the results.
Q_heating T_bottom T_top Delta_T T_mean
0.0...............250..........250........0.......250
0.002...........270..........230........40......250
0.004...........275..........225........50......250
0.01.............280..........220.......60......250
0.02.............285..........215.......70......250
0.03.............290..........210.......80......250
0.04.............300..........200.......100.....250
0.05.............305..........195.......110.....250
If the atmosphere doesn’t take part in cooling the ground it is all at 250 K. If the atmosphere do it, its temperature profile rotates around its center of mass whose temperature doesn’t vary. That’s the atmosphere doesn’t increase its total thermodynamic energy and, as the convection requires the lapse rate is –g/Cp = const, that that varies is its thickness which pass from 4000 meters at Q_heating = 0.002 to 110000 meters at Q_heating = 0.05.
The atmosphere increases its gravitational potential energy without varying the thermodynamic one. Indeed, the temperature of Heart’s atmosphere at p=0.5 bar is 255 K, i.e. the Heart’s Teff.
It’s amazing! I always believed the opposite.
Michele
Dear Michele,
ReplyDeleteThat is a fascinating experiment. I particularly like your use of the temperature difference and the adiabatic laps rate to deduce the height of the atmospheric column. I keep forgetting that the laps rate must be −g/Cp. I hope you will keep reminding me. It's such a simple result that it seems too good to be true.
So, we have concluded that the gravitational potential and the thermodynamic potential are different and can vary independently.
In your experiment, I assume that energy must go into raising the atmosphere at the beginning, so there will be heat that turns into gravitational potential energy.
How would you calculate the altitude of the center of mass at equilibrium?
Yours, Kevan
Michele,
ReplyDeleteI could, of course, answer my question above myself, but I thought you might have some clever way of doing it without integrating. Also: I have added a "Constant Flow" configuration to the program to allow others to perform your experiment (available in CC4 next post).
With this configuration, I obtained for Q_heating = 0.01 and MR=0.0, 270 K at the bottom and 225 K at the top. With MR=0.1 I obtain 276 K and 221 K. I'm using CC4, which has the work by convection added back in as viscous heat.
The addition of the viscous heat disturbs the −g/Cp. I will work on this again tomorrow.
Yours, Kevan
“Center of mass”
ReplyDeleteI was formally improper. I would refer to the point where the masses above and below are equal and the pressure is p = (p_bottom+p_top)/2, i.e. the 8th row.
“In your experiment, I assume that energy must go into raising the atmosphere at the beginning, so there will be heat that turns into gravitational potential energy.”
The answer is in the condition Qe = M(CpΔT + gΔz). The temperature at the 8th row doesn’t vary, the column expands isothermally into the gravity field and so Qe = MgΔz.
“The addition of the viscous heat disturbs the −g/Cp. I will work on this again tomorrow.”
As far I know the viscosity is always negligible for the gasses except that for the shear flow occurring in the boundary layer because the high gradient of velocity. The group of four cells would circulate more and more vertically as in an tornado.
Michele
Dear Michele,
ReplyDeleteI disagree with you about viscosity. I will endeavor to make my case in a convincing manner.
When it comes to pressure drops in pipes, and temperature changes in chemical plants, viscosity is negligible except at the boundary layer. But with turbulent flow in open fluids, where pressure drops are tiny and a 1-K change in temperature is large, viscosity is significant in the entire volume.
In turbulent flow, viscosity generates heat. Instead of a simple surface with a velocity gradient, we have a volume in which the gradient alternates within the volume. If the boundary layer in a pipe is 0.1 mm thick, we can imagine a turbulent flow with ten such boundary layers per centimeter.
Without viscosity, there would be no low-pressure region behind the blades of a windmill. (Of this I am absolutely certain.) The windmill would not turn. (It would not turn in liquid helium.) And yet windmills do turn. We see that viscosity has a significant effect upon the behavior of air even at speeds of a few meters per second with no pipe boundary.
Suppose I have a box with a propellor inside. I turn the propellor with a shaft that comes out of the box. The bearings of the shaft are perfect. The box is filled with air. I turn the propellor. It spins in the box. I let the propellor spin on its own. Eventually, it comes to a stop because of air friction. Where does the kinetic energy of my propellor go? It turns into heat in the box, by the action of viscosity. We can tell this must be the case, because without viscosity, the propellor would never slow down.
So, I say again that the small amount of work available from each circulation of cells will be dissipated as viscous friction. The approximation I am making is to say that the friction will take place within these four cells, instead of being carried away into other cells.
Yours, Kevan
Dear Michele,
ReplyDeleteI like the name "Equal Flow" better for your earlier experiment. With "Equal Flow" and no accounting for the work by convection, the array just keeps cooling down forever. With the viscous work turned on, it reaches equilibrium after a few hundred thousand iterations to 277K at bottom and 221K at top with or without mixing, and for Q=0.01K. Average is 249 K.
In your swap_cells routine, are you still adding a T_step to one cell and subtracting T_step from another? If so, you are avoiding the work by circulation, so you will see convergence, but not exactly the same convergence.
Yours, Kevan
WturheMacma Ryan Hermanson click
ReplyDeletedownload
link
https://colab.research.google.com/drive/1c2YWoAAMphlC_0mcEkyoXyiHKXcUVy7T
dyneragland
This comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDelete