Mercury Bulb, Part I

When the temperature recorded by a thermometer two meters above the desert drops by 10°C in an hour, what does this drop mean? Does it mean that the air has cooled down, or does it mean that the radiating bodies around it have cooled down? When we feel cold walking in the desert at night, is this because the air is cold, or is it because the sand all around us is no longer radiating heat that would otherwise warm our bodies? So far, we have assumed that it is the air that cooled down. In any case, we feel it is time to consider the role played by conduction, radiation, and convection in determining the temperature recorded by a mercury bulb thermometer.

Let us start with conduction. We will simplify the conduction question by considering steady-state heat flow out of a spherical mercury bulb with thin walls. By "steady-state" we mean that no element in our problem is either warming up or cooling down. The heat conducted away from the bulb is constant. The advantage of this simplification is that it has a simple analytical solution, as we show in the following diagram.



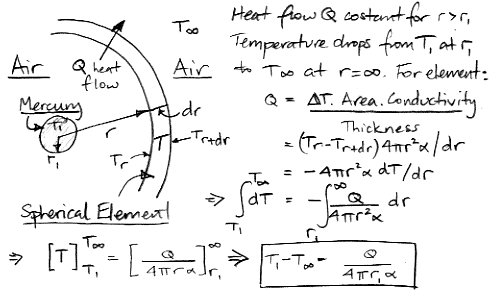
Meanwhile, the heat capacity of the bulb allows us to relate the heat flow out of the bulb to the rate at which the temperature of the bulb must be falling, as we show below. In our continuing equations, we use T and r for the temperature and radius of the bulb.



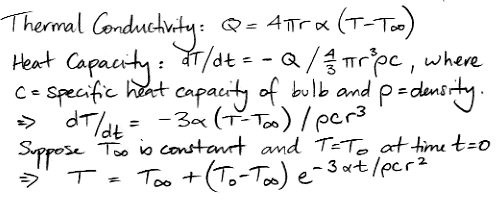
The following graph plots the temperature of mercury bulbs of various radii versus time after a sudden 10°C drop in temperature. We see that a bulb of radius 2 mm will cool to within 0.5°C of the new air temperature within a few minutes.



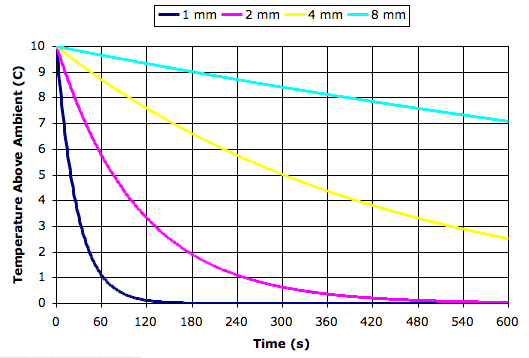
Most mercury bulbs are a few millimeters in diameter, so it appears that mercury thermometers can measure air temperature accurately provided that the changes in air temperature occur on a time scale of ten minutes or longer. In our next post we will consider whether radiation from the ground, the sun, and the bulb itself will disturb the thermometer's measurement of ambient air temperature.