Mercury Bulb, Part II

Suppose we expose our mercury bulb thermometer to radiation from the Sun and the ground, as shown below. We have short-wave radiation arriving from the Sun far away, long-wave radiation arriving from the ground just below, and the bulb radiating as well. If we assume the air below the bulb is transparent, the heat the bulb receives from the ground is equal to the heat it would receive from a hemispherical shell of the same material.



The ground and the bulb are opaque to short-wave and long-wave radiation. The emissivity of mercury is roughly 0.10 for short-wave and long-wave, while that of sand and dirt is 0.90 for both short-wave and long-wave.

In the following calculations, we use the letter ε for emissivity, and a subscript to indicate ground or bulb. The radius of the bulb is r. We calculate the net absorption of radiation by the bulb, in Watts. We assume that this extra heat will cause a slight increase in the bulb's temperature over the temperature of the air, leading to conduction of the excess heat away from the bulb. We apply the equation for steady-state conduction we derived last time, and so arrive at an equation for the change in the bulb temperature in terms of power arriving from the sun, ground temperature, and air temperature.



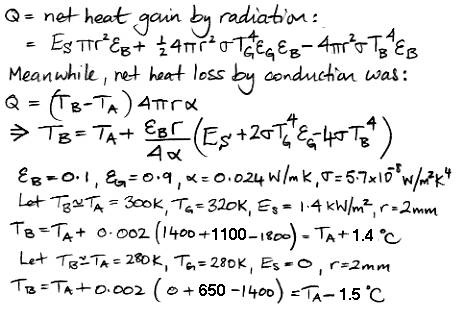
In Arizona over Thanksgiving, we observed the ground to be at around 320 K at mid-day and the air at 300 K. In Solar Heat, we showed that the power arriving from the sun is 1,400 W for each square meter we hold up perpendicular to its rays. A thermometer exposed to the sun and the ground under these conditions will read 1.5°C warmer than the air. At night, we observed the air and the ground to drop to around 280 K. A thermometer free to radiate its heat into space under these conditions will read 1.5°C colder than the air.

Suppose we house our thermometer in a box with holes on the sides to let air through, but a solid roof and floor. We make the box out of a good insulator, like wood. Air can move freely through the box, but radiation from the ground and the sun are blocked. The outside of the box may get hot during the day or cold at night, but the inside surface will settle to the air temperature, along with the thermometer bulb. The radiation the bulb receives from the box will be exactly equal to the radiation it emits towards the box.

During the day, the ground warms the air. In order for heat to pass from the ground to the air, there must be a sharp temperature gradient near the surface, because the conductivity of air is so poor. If we place our thermometer one meter above the surface, it will be out of this heating layer, and so measure the temperature of the main body of air moving along the ground. When the wind blows, the thermometer will be more effective at measuring air temperature, because the movement of air around the bulb greatly facilitates the transfer of heat to and from the bulb. But once again, the wind near the ground can be erratic, or shielded by obstacles, so placing the thermometer a meter above the ground would make sure that it experiences the temperature of the main body of moving air.

We conclude that a thermometer mounted in a perforated box one meter above the ground will give us an accurate measurement of air temperature, despite the effects of radiation, conduction, and convection.