Peter Newnam points us to an article in The Guardian discussing the implications of a recent paper, Sequestering Carbon Dioxide in a Closed Underground Volume by Economides et al. We do our best to present the content of the paper in the following paragraphs, because we cannot see the content explained anywhere else. For consistency with our other posts, we will convert the paper's imperial units to metric units.
One way to get rid of CO2 is to pump it into the ground and leave it there. Storing CO2 under the ground is called carbon dioxide sequestration. If we pump CO2 into the ground just any old place, it will leak out again. We must find a suitable geological formation that will hold and keep the CO2 indefinitely. An aquifer is an example of such a formation: a layer of permeable rock, perhaps a hundred meters thick, surrounded on all sides with impermeable rock. Aquifers are usually filled with water, oil, or natural gas.
Exhausted oil reservoirs are ideal aquifers in which to store CO2 because they have been depleted of their fluid content. Oil companies even go so far as to buy CO2 and pump it down into oil reservoirs to push the oil out. But exhausted oil reserves are already being used to store natural gas. They are not available for sequestration. Most CO2 sequestration schemes use an aquifer that is saturated with water or brine. We pump the CO2 into the aquifer at sufficient pressure to compress the water and the rock. The rock and water get smaller to make space for the CO2.
The initial pressure of almost all aquifers, before we start pumping in CO2, will be close to Hρg, where H is the aquifer depth, ρ is the density of water, and g is gravity. An aquifer 2 km down will have formation pressure close to 20 MPa = 200 Bar. Aquifers fracture if the pressure gradient from the surface to the aquifer exceeds 20 kPa/m. An aquifer at 2000 m cannot be pressurized to more than 40 MPa = 400 Bar without fracturing. When an aquifer fractures, its contents leak out.
Suppose the aquifer is initially 20% water and 80% rock. The bulk modulus of rock is roughly 70 GPa and of water is roughly 2 GPa. If we raise the pressure in the aquifer from 20 MPa to 40 MPa, the volume of the pre-existing rock and water shrinks by 0.36%. The Prudhoe Bay reservoir is the largest oil field in the United States. It is 1000 km2 in area and up to 100 m thick. Suppose our sequestration reservoir is of the same size. When we pressurize it to 40 MPa, the 1011 m3 volume of the aquifer's rock and water contracts by 360×106 m3. Meanwhile, CO2 at this pressure has density 650 kg/m3, so the maximum mass of CO2 we can store in our aquifer without fracturing its impermeable rock walls is 240×109 kg. A 500-MW coal-burning power plant produces 3×109 kg/yr. There are roughly one thousand such coal-burning plants in the US alone. One thousand reservoirs the size of Prudhoe Bay would be required to store the CO2 generated by these one thousand plants over the course of eighty years.
But the paper shows that the capacity of an aquifer is further limited by the rate at which we can inject CO2 into the aquifer. In order to force CO2 through the the porous rock, we must apply a pressure greater than the reservoir pressure, and even with 10 MPa of excess pressure, the CO2 does not rush into the aquifer. It seeps in. An aquifer five times the size of Prudhoe Bay, along with four separate injecting wells, would be required to sequester the CO2 produced by a single 500-MW coal-burning power plant.
Previous work on the subject suggested that we could push CO2 into an aquifer ten to a hundred times faster. Economidese et al. mention two problems with previous work. One problem is that previous work confused the volume of the pores in the aquifer with the volume of the aquifer. The volume of the pores is only 20% of the volume of the aquifer. This confusion led to an over-estimation of the sequestration rate by a factor of five. The other problem is that previous calculations assumed that the pressure at the boundaries of the aquifer was constant. If the pressure at the boundaries is constant, we certainly can push CO2 in faster, perhaps ten times faster. But such an assumption implies that water, and ultimately CO2, will escape the aquifer at the boundaries. In other words: you can fit a lot more CO2 into an aquifer if you allow it to leak out at the edges, but that rather defeats the purpose of sequestration.
In short: the paper concludes that carbon sequestration is impractical. The state of Rhode Island would require an aquifer as large as itself just to sequester 20% of the CO2 generated by its own electricity consumption.
UPDATE: My father is a retired chemical engineer. He was a pioneer in liquified natural gas. He designed the large LNG tank outside Boston, where I live. He also studied CO2 sequestration twenty-five years ago. He read Economides et al. and "did not think much of it". He says there are better places to put CO2 than the aquifers discussed in the paper.
Wednesday, April 28, 2010
Monday, April 26, 2010
Committees and Law Suits
Michael Mann, of Mann-Made Warming, has hired a law firm. His law firm wrote to Minnesotans for Global Warming (MGW), the makers of the Hide the Decline music video. This video uses a photograph of Dr. Mann's face. The letter from the lawyers demands that MGW stop using Dr. Mann's likeness, saying the "video clearly defames Professor Mann by leaving viewers with the incorrect impression that he falsified data to generate desired results". Youtube has removed all copies of the video, as well as a new version that does not use Dr. Mann's face. But No Cap and Trade is still hosting the original video, which I linked to earlier in this paragraph.
If Dr. Mann goes to court with MGW, his lawyers will argue that he did not fabricate measurements or data. But the defense will be able to address the definition of "data" and "measurement", and so shine light upon the idea of "value-added data" and "multi-proxy statistics". Dr. Mann combined measurements in a way that created a hockey-stick graph regardless of the input data, and even goes so far as to invert measurements that decline, so they rise instead, and contribute to the hockey-stick shape. Dr. Mann presented his Hockey Stick Graph as if it were a measurement. Either he knew full well that he was falsifying this measurement, or he became confused and did not understand his own mistake. Subsequent inquiries prompted by the work of Mr. McIntyre gave Dr. Mann ample opportunity to see his error and withdraw his graph. But Dr. Mann still insists that his graph is a useful measurement of global temperature changes over the past thousand years.
A law suit bestows the power of subpoena. Dr. Mann could be interrogated in court or during depositions. He would have to answer questions about his work. He would not be able to dismiss the inverted-measurement accusation as "bizarre" and say nothing more about it. So I hope the case goes to court. I would donate to the MGW legal fund.
Here's another law suit. Climate modeler Andrew Weaver asked Canada's National Post to "retract a number of recent articles that attributed to me statements I never made, accused me of things I never did, and attacked me for views I never held." Perhaps Mr. Weaver is referring to articles like this, in which he comes across as a conspiracy theorist. The National Post refused to retract their statements, so Mr. Weaver is suing them for "grossly irresponsible falsehoods" and for insults posted in the on-line comments.
Mr. Weaver's case looks like it will degenerate into an argument about what he said in interviews, not an argument about the science. So I'm not as enthusiastic about his law suit. I hope the paper did not misrepresent him. I image being misrepresented must be frustrating.
A second inquiry into Climategate has produced its conclusion. This inquiry was headed by Lord Oxburgh and was instigated by the University of East Anglia, home of the Climatic Research Unit (CRU) and epicenter of the entire affair. The inquiry concluded that the scientists involved did nothing wrong. This conclusion has been greeted with enthusiasm by most climatologists, such as those providing content at Realclimate, but there are some climatologists who are not satisfied by either the Oxburgh Report or the Parliamentary Report. Vocal among the critics of these reports is Judith Curry. She notes, and we agree with her, that neither report addresses any of the main issues raised by critics of climate science, such as those listed in by Mr. McIntyre in his submission to the Parliamentary Committee. But the two inquiries were supposed to identify any "wrong-doing" on the part of CRU scientists. I'm not sure what "wrong-doing" is.
The point of Climategate is that climatologists don't obey the same rules as the rest of us in other fields of science. We don't substitute instrument data for proxy data and then plot the result as if it were all proxy data (Gavin Schmidt). If I were to hide a trend using a trick, I would deserve to be fired from my position. It's not up to committees to condemn climatologists. It's up to us scientists in other fields to distance ourselves from their work so that their field can no longer lay claim to the authority that has been earned by properly-conducted science over the past three centuries.
These law suits hold more promise than the committees. In the law suits, the definition of scientific conduct would be addressed, and judges are good at understanding the logic of definitions. Let's not forget the great work done by Judge John E. Jones on the subject of intelligent design. He judged that the definition of "science" was that it addressed natural phenomena only, so any theory, such as intelligent design, which mentioned the existence of a super-natural being, was by definition non-scientific, regardless of its truth or falsehood. We need a judge like him in the Dr. Mann vs. MGW case.
If Dr. Mann goes to court with MGW, his lawyers will argue that he did not fabricate measurements or data. But the defense will be able to address the definition of "data" and "measurement", and so shine light upon the idea of "value-added data" and "multi-proxy statistics". Dr. Mann combined measurements in a way that created a hockey-stick graph regardless of the input data, and even goes so far as to invert measurements that decline, so they rise instead, and contribute to the hockey-stick shape. Dr. Mann presented his Hockey Stick Graph as if it were a measurement. Either he knew full well that he was falsifying this measurement, or he became confused and did not understand his own mistake. Subsequent inquiries prompted by the work of Mr. McIntyre gave Dr. Mann ample opportunity to see his error and withdraw his graph. But Dr. Mann still insists that his graph is a useful measurement of global temperature changes over the past thousand years.
A law suit bestows the power of subpoena. Dr. Mann could be interrogated in court or during depositions. He would have to answer questions about his work. He would not be able to dismiss the inverted-measurement accusation as "bizarre" and say nothing more about it. So I hope the case goes to court. I would donate to the MGW legal fund.
Here's another law suit. Climate modeler Andrew Weaver asked Canada's National Post to "retract a number of recent articles that attributed to me statements I never made, accused me of things I never did, and attacked me for views I never held." Perhaps Mr. Weaver is referring to articles like this, in which he comes across as a conspiracy theorist. The National Post refused to retract their statements, so Mr. Weaver is suing them for "grossly irresponsible falsehoods" and for insults posted in the on-line comments.
Mr. Weaver's case looks like it will degenerate into an argument about what he said in interviews, not an argument about the science. So I'm not as enthusiastic about his law suit. I hope the paper did not misrepresent him. I image being misrepresented must be frustrating.
A second inquiry into Climategate has produced its conclusion. This inquiry was headed by Lord Oxburgh and was instigated by the University of East Anglia, home of the Climatic Research Unit (CRU) and epicenter of the entire affair. The inquiry concluded that the scientists involved did nothing wrong. This conclusion has been greeted with enthusiasm by most climatologists, such as those providing content at Realclimate, but there are some climatologists who are not satisfied by either the Oxburgh Report or the Parliamentary Report. Vocal among the critics of these reports is Judith Curry. She notes, and we agree with her, that neither report addresses any of the main issues raised by critics of climate science, such as those listed in by Mr. McIntyre in his submission to the Parliamentary Committee. But the two inquiries were supposed to identify any "wrong-doing" on the part of CRU scientists. I'm not sure what "wrong-doing" is.
The point of Climategate is that climatologists don't obey the same rules as the rest of us in other fields of science. We don't substitute instrument data for proxy data and then plot the result as if it were all proxy data (Gavin Schmidt). If I were to hide a trend using a trick, I would deserve to be fired from my position. It's not up to committees to condemn climatologists. It's up to us scientists in other fields to distance ourselves from their work so that their field can no longer lay claim to the authority that has been earned by properly-conducted science over the past three centuries.
These law suits hold more promise than the committees. In the law suits, the definition of scientific conduct would be addressed, and judges are good at understanding the logic of definitions. Let's not forget the great work done by Judge John E. Jones on the subject of intelligent design. He judged that the definition of "science" was that it addressed natural phenomena only, so any theory, such as intelligent design, which mentioned the existence of a super-natural being, was by definition non-scientific, regardless of its truth or falsehood. We need a judge like him in the Dr. Mann vs. MGW case.
Wednesday, April 21, 2010
Work by Convection
The following diagram plots the pressure and volume of one kilogram of air taking part in the cycle we described in Atmospheric Convection.
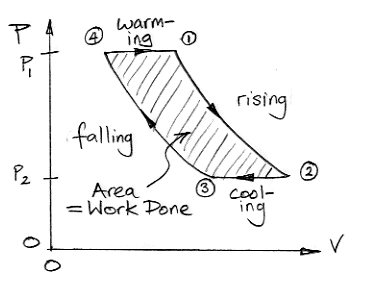
From (4) to (1) the gas warms at constant pressure while in contact with the Body. From (1) to (2) it rises through the atmosphere, expands, and cools. From (2) to (3) it cools at constant pressure in the troposphere by radiating its heat into space. From (3) to (4) it descends, contracts, and warms.
A pressure-volume plot allows us to determine the amount of work done by the air taking part in our cycle. Consider a volume of air, v, at pressure p in a cylinder with a piston. The piston has cross-section A. We let the air expand a small amount dv. The work done by the gas is equal to the force on the piston, pA, multiplied by the distance the piston moves, dv/A. So the work done is pdv. This relation holds regardless of the shape of the gas volume as it expands by dv at pressure p. The work done is equal to the integral of pressure with respect to volume, which is the area under the plot of pressure versus volume.
The area under the plot from (4) to (2) is the work done by the gas as it expands. The gas does work compressing the surrounding atmosphere. The area under the plot from (2) to (4) is the work done upon the gas as it contracts. The surrounding atmosphere does work to compress the gas. The amount of work done by the warm, expanding gas is greater than the amount of work required to compress the cool gas. The area enclosed by the pressure-volume plot is positive. Not only does the convection cycle transport heat up through the atmosphere, it also does work.
We could place windmills or turbines in the way of the air that rises and falls in our convection cycle, and so extract work from the cycle. Where does the energy for this work come from? There are no windmills or turbines in the way of the air in our extreme greenhouse, so what happens to the work produced by the convection cycle?
We will try to answer these questions in our next post on the subject.

From (4) to (1) the gas warms at constant pressure while in contact with the Body. From (1) to (2) it rises through the atmosphere, expands, and cools. From (2) to (3) it cools at constant pressure in the troposphere by radiating its heat into space. From (3) to (4) it descends, contracts, and warms.
A pressure-volume plot allows us to determine the amount of work done by the air taking part in our cycle. Consider a volume of air, v, at pressure p in a cylinder with a piston. The piston has cross-section A. We let the air expand a small amount dv. The work done by the gas is equal to the force on the piston, pA, multiplied by the distance the piston moves, dv/A. So the work done is pdv. This relation holds regardless of the shape of the gas volume as it expands by dv at pressure p. The work done is equal to the integral of pressure with respect to volume, which is the area under the plot of pressure versus volume.
The area under the plot from (4) to (2) is the work done by the gas as it expands. The gas does work compressing the surrounding atmosphere. The area under the plot from (2) to (4) is the work done upon the gas as it contracts. The surrounding atmosphere does work to compress the gas. The amount of work done by the warm, expanding gas is greater than the amount of work required to compress the cool gas. The area enclosed by the pressure-volume plot is positive. Not only does the convection cycle transport heat up through the atmosphere, it also does work.
We could place windmills or turbines in the way of the air that rises and falls in our convection cycle, and so extract work from the cycle. Where does the energy for this work come from? There are no windmills or turbines in the way of the air in our extreme greenhouse, so what happens to the work produced by the convection cycle?
We will try to answer these questions in our next post on the subject.
Wednesday, April 14, 2010
Atmopsheric Convection
Consider the following diagram. It shows a large volume of dry air taking part in a convection cycle above the Body in our Extreme Greenhouse.
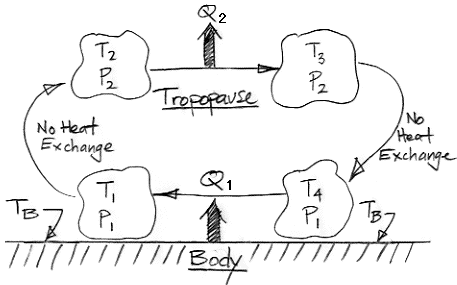
At Point 1, on the lower-left, the Volume has been warmed by contact with the Body. The Body itself, we recall, is being warmed by short-wave radiation from the Sun. This is an extreme greenhouse, so let's choose T1 = 400 K, TB = 405 K, and p1 = 100 kPa.
The Volume is now so warm that it is less dense than the lower-pressure air above. The Volume rises through the atmosphere. This atmosphere is black to long-wave radiation. The Volume emits and absorbs long-wave radiation, but it rises quickly enough that any imbalance in the radiation it emits and absorbs is negligible compared to the heat it absorbed from the Body. As the Volume rises, it mixes with other volumes of air at its borders. We assume the Volume is so large and rises so quickly that whatever happens at its borders is negligible compared to the vast bulk of the Volume within.
In short, we assume that any heat entering or leaving the Volume on the way up is negligible. The expansion of the Volume will be adiabatic. As a gas expands adiabatically, it cools down, even though no heat passes out of it. Given a particular pressure drop from adiabatic expansion in a particular gas, we can determine the corresponding change in temperature. Our Extreme Greenhouse atmosphere is mostly nitrogen and oxygen, both of which are diatomic molecules, and we have assumed our Volume is dry. In the adiabatic expansion of diatomic gases, p 0.4T −1.4 is constant, where p and T are the absolute pressure and absolute temperature of the gas respectively.
The Volume rises until it reaches the tropopause, which is Point 2 in the diagram. As we showed in an earlier post, the tropopause in our Extreme Greenhouse corresponds to the upper surface of the Filter Gas, and is at pressure p2 = 30 kPa. The Volume expanded adiabatically, so its temperature must now be T2 = 285 K.
At the tropopause, heat starts to leave the Volume. Heat leaves by radiation directly into space because there is too little atmosphere above the tropopause to absorb all the Volume's outward radiation. The Volume becomes more dense. It stops rising and it cools at constant pressure. At Point 3, the Volume has cooled until it is so dense that it starts to fall through the higher-pressure air below. Suppose it has cooled by 10 K so that T3 = 275 K.
Just as we assumed adiabatic expansion as the Volume rose, we now assume adiabatic compression as it falls. As the Volume descends to Point 4, its pressure increases from 30 kPa to 100 kPa, so its temperature must rise to T4 = 385 K. When it arrives at the surface, the Volume is once again in contact with the Body, which is at TB = 405 K. A typical value for the coefficient of heat transfer between a rough surface and moving air is 50 W/m2K. With this value, heat starts to flow from the Body to the Volume at 1000 W/m2. The Volume warms up. When it reaches T1 = 400 K, heat flows at 250 W/m2. At this temperature, however, the gas is light enough to rise. We have returned to Point 1 in our diagram, and the convection cycle begins again.
As we established in previous posts, the temperature of the tropopause in our Extreme Greenhouse depends only upon the amount of long-wave radiation it must emit into space, which is exactly equal to the amount of short-wave radiation absorbed by the Body from the Sun. In our Extreme Greenhouse, the tropopause must be at 280 K. In our convection cycle, the Volume cools from 285 K to 275 K in the tropopause. Its average temperature is 280 K. As its descends, it warms up by 115 K.
The atmosphere of our Extreme Greenhouse must transport 350 W/m2 from the Body to the tropopause, because this is the amount of heat the Body receives from the Sun. But we need less than a 10-K difference between the Volume and the Body to obtain this heat flow. This 10-K difference is small compared to the 115-K difference between the surface and the tropopause. We see that the temperature difference between the Body and the tropopause is dominated by the temperature difference required to drive convective cooling by adiabatic expansion. To the first approximation, the temperature difference between the Body and the tropopause does not depend upon the amount of heat that the atmosphere must transport. To the first approximation, the size of the greenhouse effect depends only upon the temperature of the tropopause and the ratio of the tropopause pressure to the surface pressure.
In our example, the tropopause pressure is 30% of the surface pressure so that the surface temperature must be 140% of the tropopause temperature. If the surface temperature were any lower, there would be no convective heat transport to the troposphere, and the Body would get hotter until convection started.
The pressure of the tropopause, meanwhile, depends upon the long-wave absorption spectrum of the atmosphere. In our Extreme Greenhouse, the atmosphere is black to all long-wave radiation because of a greenhouse gas mixed in with its nitrogen and oxygen. When we double the concentration of this greenhouse gas, the tropopause pressure drops from 30 kPa to 15 kPa. Its altitude rises from 12 km to 17.5 km. But the tropopause temperature must still be 280 K. After this doubling of concentration, the Body temperature must rise to 170% of 280 K, or 480 K. A doubling of greenhouse gas concentration raises the Body temperature by 75°C.

At Point 1, on the lower-left, the Volume has been warmed by contact with the Body. The Body itself, we recall, is being warmed by short-wave radiation from the Sun. This is an extreme greenhouse, so let's choose T1 = 400 K, TB = 405 K, and p1 = 100 kPa.
The Volume is now so warm that it is less dense than the lower-pressure air above. The Volume rises through the atmosphere. This atmosphere is black to long-wave radiation. The Volume emits and absorbs long-wave radiation, but it rises quickly enough that any imbalance in the radiation it emits and absorbs is negligible compared to the heat it absorbed from the Body. As the Volume rises, it mixes with other volumes of air at its borders. We assume the Volume is so large and rises so quickly that whatever happens at its borders is negligible compared to the vast bulk of the Volume within.
In short, we assume that any heat entering or leaving the Volume on the way up is negligible. The expansion of the Volume will be adiabatic. As a gas expands adiabatically, it cools down, even though no heat passes out of it. Given a particular pressure drop from adiabatic expansion in a particular gas, we can determine the corresponding change in temperature. Our Extreme Greenhouse atmosphere is mostly nitrogen and oxygen, both of which are diatomic molecules, and we have assumed our Volume is dry. In the adiabatic expansion of diatomic gases, p 0.4T −1.4 is constant, where p and T are the absolute pressure and absolute temperature of the gas respectively.
The Volume rises until it reaches the tropopause, which is Point 2 in the diagram. As we showed in an earlier post, the tropopause in our Extreme Greenhouse corresponds to the upper surface of the Filter Gas, and is at pressure p2 = 30 kPa. The Volume expanded adiabatically, so its temperature must now be T2 = 285 K.
At the tropopause, heat starts to leave the Volume. Heat leaves by radiation directly into space because there is too little atmosphere above the tropopause to absorb all the Volume's outward radiation. The Volume becomes more dense. It stops rising and it cools at constant pressure. At Point 3, the Volume has cooled until it is so dense that it starts to fall through the higher-pressure air below. Suppose it has cooled by 10 K so that T3 = 275 K.
Just as we assumed adiabatic expansion as the Volume rose, we now assume adiabatic compression as it falls. As the Volume descends to Point 4, its pressure increases from 30 kPa to 100 kPa, so its temperature must rise to T4 = 385 K. When it arrives at the surface, the Volume is once again in contact with the Body, which is at TB = 405 K. A typical value for the coefficient of heat transfer between a rough surface and moving air is 50 W/m2K. With this value, heat starts to flow from the Body to the Volume at 1000 W/m2. The Volume warms up. When it reaches T1 = 400 K, heat flows at 250 W/m2. At this temperature, however, the gas is light enough to rise. We have returned to Point 1 in our diagram, and the convection cycle begins again.
As we established in previous posts, the temperature of the tropopause in our Extreme Greenhouse depends only upon the amount of long-wave radiation it must emit into space, which is exactly equal to the amount of short-wave radiation absorbed by the Body from the Sun. In our Extreme Greenhouse, the tropopause must be at 280 K. In our convection cycle, the Volume cools from 285 K to 275 K in the tropopause. Its average temperature is 280 K. As its descends, it warms up by 115 K.
The atmosphere of our Extreme Greenhouse must transport 350 W/m2 from the Body to the tropopause, because this is the amount of heat the Body receives from the Sun. But we need less than a 10-K difference between the Volume and the Body to obtain this heat flow. This 10-K difference is small compared to the 115-K difference between the surface and the tropopause. We see that the temperature difference between the Body and the tropopause is dominated by the temperature difference required to drive convective cooling by adiabatic expansion. To the first approximation, the temperature difference between the Body and the tropopause does not depend upon the amount of heat that the atmosphere must transport. To the first approximation, the size of the greenhouse effect depends only upon the temperature of the tropopause and the ratio of the tropopause pressure to the surface pressure.
In our example, the tropopause pressure is 30% of the surface pressure so that the surface temperature must be 140% of the tropopause temperature. If the surface temperature were any lower, there would be no convective heat transport to the troposphere, and the Body would get hotter until convection started.
The pressure of the tropopause, meanwhile, depends upon the long-wave absorption spectrum of the atmosphere. In our Extreme Greenhouse, the atmosphere is black to all long-wave radiation because of a greenhouse gas mixed in with its nitrogen and oxygen. When we double the concentration of this greenhouse gas, the tropopause pressure drops from 30 kPa to 15 kPa. Its altitude rises from 12 km to 17.5 km. But the tropopause temperature must still be 280 K. After this doubling of concentration, the Body temperature must rise to 170% of 280 K, or 480 K. A doubling of greenhouse gas concentration raises the Body temperature by 75°C.
Monday, April 12, 2010
Ecocide
This Sunday's Guardian tells us of an effort by This is Ecocide to get the UN to recognize a fifth form of crime against humanity. They call the new crime "ecocide". On their solution page, Ecocide tells us that "ecocide can be the outcome of external factors, such as flooding or an earthquake".
If an earthquake occurs, I'm guessing the Earth's tectonic plates are to blame. It's not clear how any criminal group could cause an earthquake and then be prosecuted for it. Maybe if they did it with a thermonuclear weapon, but we already have laws against letting off thermonuclear weapons. If a flood occurs, I'm guessing it's the weather that's to blame. It's not clear how any criminal group could be prosecuted for that.
But they must have had someone in mind when they said a flood could be ecocide. What did they have in mind? What if a group of people prevent, by deliberate misinformation, the passage of laws that would otherwise have prevented the flood? What if a group of climate skeptics prevented the passage of a law that would reduce carbon dioxide emissions? Would they be guilty of ecocide?
I don't think the ecocide law would work well with the US constitution.
UPDATE: Is the volcanic eruption in iceland an act of ecocide, and if so, who is responsible?
If an earthquake occurs, I'm guessing the Earth's tectonic plates are to blame. It's not clear how any criminal group could cause an earthquake and then be prosecuted for it. Maybe if they did it with a thermonuclear weapon, but we already have laws against letting off thermonuclear weapons. If a flood occurs, I'm guessing it's the weather that's to blame. It's not clear how any criminal group could be prosecuted for that.
But they must have had someone in mind when they said a flood could be ecocide. What did they have in mind? What if a group of people prevent, by deliberate misinformation, the passage of laws that would otherwise have prevented the flood? What if a group of climate skeptics prevented the passage of a law that would reduce carbon dioxide emissions? Would they be guilty of ecocide?
I don't think the ecocide law would work well with the US constitution.
UPDATE: Is the volcanic eruption in iceland an act of ecocide, and if so, who is responsible?
Thursday, April 8, 2010
Atmospheric Temperature
In our Atmospheric Pressure post, we calculated atmospheric pressure as a function of altitude. To simplify our calculation, we assumed the temperature of the atmosphere was constant with altitude. This assumption is correct for a transparent atmosphere, but it is not correct for our Extreme Greenhouse. Nevertheless, we showed that the assumption leads to an error of no more than ±20% in our calculation of pressure even in our Extreme Greenhouse.
Today we consider how the temperature drop with altitude is related to the amount of heat transported upwards by the atmosphere. Here is our most recent Extreme Greenhouse diagram.
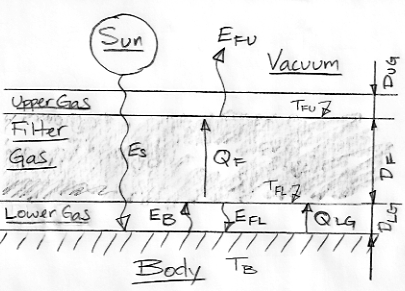
We have a Body heated uniformly by short-wave radiation from the Sun. The Body radiates heat in the form of long-wave radiation and is covered by an atmosphere divided into three layers. The transparent Lower Gas is our way of modeling the gradual absorption of long-wave radiation by the atmosphere, while the transparent Upper Gas is our way of modeling the gradual release of long-wave radiation into space.
The Filter Gas differs from the Earth's atmosphere in one important respect: the Earth's atmosphere is transparent to some bands of long-wave radiation, while our Filter Gas is opaque to all long-wave radiation. In future posts, we will make a series of modifications to our Extreme Greenhouse, so as to turn it into an adequate model of the Earth's atmosphere. But for now, the Filter Gas is black to all long-wave radiation, so its upper surface radiates all the Body's heat into space. As we showed earlier, we have EFU = ES = σ(TFU)4. With ES = 350 W/m2, we have TFU = 280 K = 7°C.
If the atmosphere were a perfect transporter of heat, we would have TB = TFU. But the atmosphere transports heat only if TB > TFU. For TFU = 7°C and ES = 350 W/m2, we estimated TB = 117°C.
The temperature drop with altitude continues until we arrive at the layer of the atmosphere that radiates heat into space. In our example, this layer is the upper surface of the Filter Gas. In the Earth's atmosphere this layer is the tropopause, where the temperature of the atmosphere stops cooling with altitude. In our original calculations, we assumed that there existed a simple relationship between the amount of heat transported by the atmosphere and the temperature drop across it. Later, in Radiation, Convection, Conduction we found that convection is the dominant source of heat transport in the atmosphere. Furthermore, when engineers calculate the heat lost from a surface by convection, they use the difference between the surface temperature and the ambient air temperature, but they do not consider the distance over which the heated air must transport the heat.
To the first approximation, convection appears to be a means of transporting heat that is hardly affected by the distance over which the heat must be moved. In this respect, convection is similar to radiation. When we calculate how much heat a body loses by radiation, we don't consider how far the radiation is going to travel before it is absorbed. The radiation could travel forever through space with no effect upon the process of emission.
In our next post, we will attempt to answer the following questions. Does the temperature drop across the atmosphere increase in proportion to the amount of heat it must transport? If the radiating surface of our atmosphere rises from 12 km to 18 km, does this increase the temperature drop? If so, by how much?
Today we consider how the temperature drop with altitude is related to the amount of heat transported upwards by the atmosphere. Here is our most recent Extreme Greenhouse diagram.

We have a Body heated uniformly by short-wave radiation from the Sun. The Body radiates heat in the form of long-wave radiation and is covered by an atmosphere divided into three layers. The transparent Lower Gas is our way of modeling the gradual absorption of long-wave radiation by the atmosphere, while the transparent Upper Gas is our way of modeling the gradual release of long-wave radiation into space.
The Filter Gas differs from the Earth's atmosphere in one important respect: the Earth's atmosphere is transparent to some bands of long-wave radiation, while our Filter Gas is opaque to all long-wave radiation. In future posts, we will make a series of modifications to our Extreme Greenhouse, so as to turn it into an adequate model of the Earth's atmosphere. But for now, the Filter Gas is black to all long-wave radiation, so its upper surface radiates all the Body's heat into space. As we showed earlier, we have EFU = ES = σ(TFU)4. With ES = 350 W/m2, we have TFU = 280 K = 7°C.
If the atmosphere were a perfect transporter of heat, we would have TB = TFU. But the atmosphere transports heat only if TB > TFU. For TFU = 7°C and ES = 350 W/m2, we estimated TB = 117°C.
The temperature drop with altitude continues until we arrive at the layer of the atmosphere that radiates heat into space. In our example, this layer is the upper surface of the Filter Gas. In the Earth's atmosphere this layer is the tropopause, where the temperature of the atmosphere stops cooling with altitude. In our original calculations, we assumed that there existed a simple relationship between the amount of heat transported by the atmosphere and the temperature drop across it. Later, in Radiation, Convection, Conduction we found that convection is the dominant source of heat transport in the atmosphere. Furthermore, when engineers calculate the heat lost from a surface by convection, they use the difference between the surface temperature and the ambient air temperature, but they do not consider the distance over which the heated air must transport the heat.
To the first approximation, convection appears to be a means of transporting heat that is hardly affected by the distance over which the heat must be moved. In this respect, convection is similar to radiation. When we calculate how much heat a body loses by radiation, we don't consider how far the radiation is going to travel before it is absorbed. The radiation could travel forever through space with no effect upon the process of emission.
In our next post, we will attempt to answer the following questions. Does the temperature drop across the atmosphere increase in proportion to the amount of heat it must transport? If the radiating surface of our atmosphere rises from 12 km to 18 km, does this increase the temperature drop? If so, by how much?
Subscribe to:
Comments (Atom)
