Atmospheric Temperature

In our Atmospheric Pressure post, we calculated atmospheric pressure as a function of altitude. To simplify our calculation, we assumed the temperature of the atmosphere was constant with altitude. This assumption is correct for a transparent atmosphere, but it is not correct for our Extreme Greenhouse. Nevertheless, we showed that the assumption leads to an error of no more than ±20% in our calculation of pressure even in our Extreme Greenhouse.

Today we consider how the temperature drop with altitude is related to the amount of heat transported upwards by the atmosphere. Here is our most recent Extreme Greenhouse diagram.



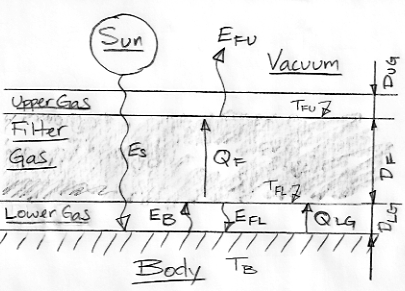
We have a Body heated uniformly by short-wave radiation from the Sun. The Body radiates heat in the form of long-wave radiation and is covered by an atmosphere divided into three layers. The transparent Lower Gas is our way of modeling the gradual absorption of long-wave radiation by the atmosphere, while the transparent Upper Gas is our way of modeling the gradual release of long-wave radiation into space.

The Filter Gas differs from the Earth's atmosphere in one important respect: the Earth's atmosphere is transparent to some bands of long-wave radiation, while our Filter Gas is opaque to all long-wave radiation. In future posts, we will make a series of modifications to our Extreme Greenhouse, so as to turn it into an adequate model of the Earth's atmosphere. But for now, the Filter Gas is black to all long-wave radiation, so its upper surface radiates all the Body's heat into space. As we showed earlier, we have E_FU = E_S = σ(T_FU)⁴. With E_S = 350 W/m², we have T_FU = 280 K = 7°C.

If the atmosphere were a perfect transporter of heat, we would have T_B = T_FU. But the atmosphere transports heat only if T_B > T_FU. For T_FU = 7°C and E_S = 350 W/m², we estimated T_B = 117°C.

The temperature drop with altitude continues until we arrive at the layer of the atmosphere that radiates heat into space. In our example, this layer is the upper surface of the Filter Gas. In the Earth's atmosphere this layer is the tropopause, where the temperature of the atmosphere stops cooling with altitude. In our original calculations, we assumed that there existed a simple relationship between the amount of heat transported by the atmosphere and the temperature drop across it. Later, in Radiation, Convection, Conduction we found that convection is the dominant source of heat transport in the atmosphere. Furthermore, when engineers calculate the heat lost from a surface by convection, they use the difference between the surface temperature and the ambient air temperature, but they do not consider the distance over which the heated air must transport the heat.

To the first approximation, convection appears to be a means of transporting heat that is hardly affected by the distance over which the heat must be moved. In this respect, convection is similar to radiation. When we calculate how much heat a body loses by radiation, we don't consider how far the radiation is going to travel before it is absorbed. The radiation could travel forever through space with no effect upon the process of emission.

In our next post, we will attempt to answer the following questions. Does the temperature drop across the atmosphere increase in proportion to the amount of heat it must transport? If the radiating surface of our atmosphere rises from 12 km to 18 km, does this increase the temperature drop? If so, by how much?