On a typical spring day at latitude 30°N, our TEP2 program tells us that the formation of high clouds will tend to warm the Earth's surface by 38°C, while the formation of thick clouds will tend to cool the Earth's surface by 96°C.
Over the past few weeks here in Boston, the warmest days have been those with high, thin clouds, and the coolest have been those with low, thick clouds. But the difference between the warm days and the cold days is only 10°C. Despite alternating clouds, rain, and sunshine, the temperature at a particular location anywhere in the world is almost always within 10°C of its monthly average at mid-day, and these monthly averages vary by less than 1°C from one year to the next.
How can it be that the Earth's surface temperature remains so stable when clouds have such tremendous power to heat and cool the surface? Some kind of self-regulation of cloud formation and evaporation must be taking place. Indeed, at first glance it seems to us that warmth will promote evaporation from the oceans and lead to the formation of the low, thick clouds that cool the Earth, while cold will suppress evaporation, encourage atmospheric convection, and lead to the formation of the high, thin clouds that warm the Earth. So each type of cloud tends to promote the formation of the other, which is a basis for self-regulation.
An example of self-regulation is the action of a thermostat in a house's heating system. When the heater turns on, the house warms up. If the heater stays on, the house will get too hot. The thermostat turns off the heater when the house is warm enough. The house cools down. If the heater stays off, the house will get too cold. The thermostat turns on the heater when the house has cooled enough. The difference between the turn-on and turn-off temperatures is the hysteresis. The temperature half-way between is the set-point.
The heating system in our house can heat the inside to 30°C when the outside is at 0°C. With the heater off, the house will eventually cool to 0°C. But our house is always close to 20°C inside. That's because the set-point of our thermostat is 20°C and its hysteresis is only 1°C.
High clouds at latitude 30°N in spring would heat the Earth to 55°C if the day were long enough and no change to the high clouds took place. Thick clouds would cool the Earth to −79°C. But the mid-day temperature remains within ±5°C of 17°C. The set-point of cloud self-regulation is roughly 17°C and its hysteresis is 10°C. The self-regulation reduces a maximum possible variation of 134°C to an observed variation of 10°C. That's a factor of thirteen reduction through self-regulation.
Our TEP2 program tells us that if we double the CO2 concentration in the atmosphere, the Earth's surface will tend to warm up by 1.5°C. Given the strong self-regulation of warming and cooling by clouds, how much warming will we actually observe if we double the CO2 concentration? It may be that the self-regulation of clouds is entirely independent of the heat retained by extra CO2, so that doubling the CO2 will increase the average temperature of the Earth's surface by a full 1.5°C.
But cloud self-regulation is not independent of the heat absorbed by extra CO2. According to our calculations, doubling the CO2 concentration of the atmosphere causes the atmosphere to retain an additional 5.0 W/m2 of heat. According to our typical atmospheric conditions, air close to the surface contains 1% water vapor, which amounts to roughly 10 g/m3. When this water condenses into water droplets, thus forming a cloud, the water vapor gives up 20 kJ/m3 of latent heat. If this condensation takes place over 1000 s (about fifteen minutes) in a column 1000 m high, it generates 20 kW/m2, which is four thousand times the heat retained by our extra CO2. The heat retained by extra CO2 and the heat produced by condensation are exactly the same type of heat. They are indistinguishable. We think it likely, therefore, that cloud self-regulation will reduce the effect of extra CO2 in the same way that it reduces the effect of cloud variation: by a factor of thirteen. In that case, doubling CO2 concentration will warm up the world by only 0.1°C.
In the presence self-regulation, however, we cannot assume even that CO2 doubling will have a net warming effect. Our calculations show that the extra CO2 causes the heat to be retained mostly between altitudes 3 km and 6 km. In an earlier post we showed how turning on an electric heater in the same room as your home's thermostat will cause the the rest of the house to cool down. It could be that the heat retained by CO2, by virtue of being concentrated in the middle-troposphere, affects cloud self-regulation in such a way as to cause a slight cooling of the surface of the Earth below. Such an outcome seems unlikely, but it is possible.
Another possibility suggested by documents like this one is that the 1.5°C warming from CO2 doubling will in fact be amplified by the self-regulation of clouds, so that we see a 3°C or even 4°C warming due to CO2 doubling. We can think of no examples of such behavior by self-regulating systems, nor do we understand the arguments presented by climatologists who propose such amplification.
In future posts we hope to explore the sources of self-regulation by clouds, and perhaps construct a simple model to investigate how the average temperature of the self-regulated system will be affected by such things as CO2 concentration and the availability of water. Before that, however, we will test our climate model by applying it to day-night variations, and to the planet Venus.
Sunday, October 31, 2010
Tuesday, October 26, 2010
Thick Clouds
We have been using our computer program, TEP2 to estimate how much the Earth's surface will tend to warm up if we make certain permanent changes to its atmosphere. In With 660 ppm CO2 we found that doubling the atmosphere's CO2 concentration from 330 ppm to 660 ppm tends to warm the Earth's surface by 1.5°C. In High Clouds we found that the formation of high, thin clouds in a clear sky will tend to warm the Earth's surface by 38°C.
Today we consider the effect of thick clouds. We start with the Earth on a typical clear spring day at latitude 30°N, as represented by our EA1.txt absorption spectra. Our TEP2 program tells us that the total escaping power is 252.5 W/m2. We allow a thick cloud to form from altitude 3 km to 12 km. In Clouds we argued that a cloud this thick will reflect 90% of the Sun's radiation and absorb 100% of the Earth's radiation. We simulate such a cloud by setting the absorption of our 3-km, 6-km, and 9-km layers to 1.0 for wavelengths 5 μm to 60 μm to produce EA4. We apply TEP2 to EA4 and obtain the following output.
As we did in High Clouds, let us suppose that the Earth radiates as much heat as it absorbs when its surface and atmosphere are as described by EA1. The total power escaping the earth is 252.5 W/m2, so the total power arriving from the Sun must be 252.5 W/m2 also. In the conditions described by EA4, 90% of the heat arriving from the Sun is reflected back into space, so only 25.2 W/m2 is absorbed by the Earth. But the total power escaping the Earth is 136.5 W/m2. When these large clouds form, the Earth will start to radiate 111 W/m2 more than it absorbs. It will cool down. In our TEP2 program, we decrease the temperature of the Earth and its atmosphere until we arrive at the following output.
According to our simulation, the formation of a 9-km thick layer of cloud at altitude 3 km has a cooling effect sixty-four times stronger than the warming effect of doubling the atmosphere's CO2 concentration.
UPDATE: When we look at discussions like this one about clouds, we see that climatologists recognize the power of clouds to cool and warm the Earth. But we don't see them giving us values in Centigrade in the same way that they do for a hypothetical doubling of CO2 concentration.
Today we consider the effect of thick clouds. We start with the Earth on a typical clear spring day at latitude 30°N, as represented by our EA1.txt absorption spectra. Our TEP2 program tells us that the total escaping power is 252.5 W/m2. We allow a thick cloud to form from altitude 3 km to 12 km. In Clouds we argued that a cloud this thick will reflect 90% of the Sun's radiation and absorb 100% of the Earth's radiation. We simulate such a cloud by setting the absorption of our 3-km, 6-km, and 9-km layers to 1.0 for wavelengths 5 μm to 60 μm to produce EA4. We apply TEP2 to EA4 and obtain the following output.
------------------------------------------------This output is exactly the same as the one we obtained for high clouds. Both the high clouds and the thick clouds have the same effect upon the total escaping heat. The difference between high clouds and thick clouds is that thick clouds block 90% of the Sun's heat from reaching the Earth, while high clouds block only 10%.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 290.0 401.1 388.8 0.0
0-km 280.0 348.5 262.6 0.0
3-km 270.0 301.3 292.0 0.0
6-km 250.0 221.5 214.0 0.0
9-km 230.0 158.7 152.3 120.8
12-km 220.0 132.8 22.2 10.1
15-km 220.0 132.8 14.4 5.5
------------------------------------------------
Total: 136.5
------------------------------------------------
As we did in High Clouds, let us suppose that the Earth radiates as much heat as it absorbs when its surface and atmosphere are as described by EA1. The total power escaping the earth is 252.5 W/m2, so the total power arriving from the Sun must be 252.5 W/m2 also. In the conditions described by EA4, 90% of the heat arriving from the Sun is reflected back into space, so only 25.2 W/m2 is absorbed by the Earth. But the total power escaping the Earth is 136.5 W/m2. When these large clouds form, the Earth will start to radiate 111 W/m2 more than it absorbs. It will cool down. In our TEP2 program, we decrease the temperature of the Earth and its atmosphere until we arrive at the following output.
------------------------------------------------Here we see the total escaping heat is 26.3 W/m2, which is pretty close to the 25.2 W/m2 arriving from the Sun through the thick clouds. The Earth's surface has cooled by 96°C.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 194.3 80.8 76.0 0.0
0-km 187.6 70.2 59.0 0.0
3-km 180.9 60.7 56.4 0.0
6-km 167.5 44.6 40.8 0.0
9-km 154.1 32.0 28.7 22.3
12-km 147.4 26.8 4.5 2.9
15-km 147.4 26.8 2.1 1.1
------------------------------------------------
Total: 26.3
------------------------------------------------
According to our simulation, the formation of a 9-km thick layer of cloud at altitude 3 km has a cooling effect sixty-four times stronger than the warming effect of doubling the atmosphere's CO2 concentration.
UPDATE: When we look at discussions like this one about clouds, we see that climatologists recognize the power of clouds to cool and warm the Earth. But we don't see them giving us values in Centigrade in the same way that they do for a hypothetical doubling of CO2 concentration.
Monday, October 18, 2010
High Clouds
Sitting on a plane over the Atlantic Ocean last month, I was at 13,000 m looking down on a continuous layer of thin, high cloud. Through occasional openings, the ocean below appeared brightly-lit despite the clouds above it. Today we estimate the effect of such a cloud layer upon total escaping power using our TEP2 program.
Let us place a 1-km thick layer of cloud in our 9-km atmospheric layer. This layer extends from altitude 9 km to 12 km. In our previous post we showed that a 1-km thick layer of cloud absorbs 100% of incident long-wave radiation, but only 10% of incident short-wave radiation. In our atmospheric absorption spectra we simulate such a cloud by setting the absorption of our 9-km layer to 1.0 for wavelengths 5 μm to 60 μm. We start with our EA1 spectra (typical, clear, spring day at 30°N) and produce EA3. We submit EA3 to TEP2 and obtain the following table of escaping power in W/m2. We add the final column by hand, which gives the change in escaping power caused by the introduction of the cloud.
We note that the black-body radiation for our 9-km layer is 158.7 W/m2 (BB column) while the heat that TEP2 calculates by numerical integration is only 152.3 W/m2 (Layer column). Our spectra extend to 60 μm, but the cool cloud (−43°C) radiates some power in the range 60-100 μm. We will accept this 4% error and move on.
The cloud causes the total escaping power to drop by 116 W/m2, or 46%. We now ask how much warmer the Earth's surface will have to get in order to make up a 46% drop in total escaping power caused by the formation of a 1-km layer of cloud at altitude 10 km. The 1-km cloud absorbs some of the heat arriving from the Sun, and we must take this into account somehow when we perform our estimate.
Let us suppose that the Earth radiates as much heat as it absorbs when its surface and atmosphere are as described by EA1. Because the Earth and its atmosphere radiate a total of of 252.5 W/m2, we suppose that a like amount of heat arrives from the Sun and lands upon the Earth's surface. When we place a 1-km layer of cloud in the way, we estimate that 10% of the Sun's heat will be reflected back out into space. When the cloud layer forms, the heat arriving from the Sun decreases to 227 W/m2 and the heat escaping from the Earth decreases to 136 W/m2.
By experimenting with TEP2, we find that a 13% increase in the absolute temperature of the Earth and its atmospheric layers will produce the following result.
According to our simulation, the formation of a 1-km thick layer of cloud at altitude 10 km has twenty-five times the warming effect as doubling the atmosphere's CO2 concentration.
UPDATE: Michele points out that high clouds will contain microscopic ice particles instead of water droplets. Ice, like water, is also opaque to long-wave radiation and transparent to short-wave radiation.
Let us place a 1-km thick layer of cloud in our 9-km atmospheric layer. This layer extends from altitude 9 km to 12 km. In our previous post we showed that a 1-km thick layer of cloud absorbs 100% of incident long-wave radiation, but only 10% of incident short-wave radiation. In our atmospheric absorption spectra we simulate such a cloud by setting the absorption of our 9-km layer to 1.0 for wavelengths 5 μm to 60 μm. We start with our EA1 spectra (typical, clear, spring day at 30°N) and produce EA3. We submit EA3 to TEP2 and obtain the following table of escaping power in W/m2. We add the final column by hand, which gives the change in escaping power caused by the introduction of the cloud.
-------------------------------------------------------No radiation escapes into space from the Earth's surface or from the first three layers of the atmosphere. A total of 210.4 W/m2 is absorbed by the lower surface of the cloud layer. The cloud layer itself, however, is a fine radiator of heat, and radiates 120.8 W/m2 into space.
Name Temp BB Layer Escaping Change
-------------------------------------------------------
Surface 290.0 401.1 388.8 0.0 -80.0
0-km 280.0 348.5 262.6 0.0 -46.1
3-km 270.0 301.3 184.8 0.0 -39.7
6-km 250.0 221.5 111.5 0.0 -44.6
9-km 230.0 158.7 152.3 120.8 94.4
12-km 220.0 132.8 22.2 10.1 0.0
15-km 220.0 132.8 14.4 5.5 0.0
-------------------------------------------------------
Total: 136.5 -116.0
-------------------------------------------------------
We note that the black-body radiation for our 9-km layer is 158.7 W/m2 (BB column) while the heat that TEP2 calculates by numerical integration is only 152.3 W/m2 (Layer column). Our spectra extend to 60 μm, but the cool cloud (−43°C) radiates some power in the range 60-100 μm. We will accept this 4% error and move on.
The cloud causes the total escaping power to drop by 116 W/m2, or 46%. We now ask how much warmer the Earth's surface will have to get in order to make up a 46% drop in total escaping power caused by the formation of a 1-km layer of cloud at altitude 10 km. The 1-km cloud absorbs some of the heat arriving from the Sun, and we must take this into account somehow when we perform our estimate.
Let us suppose that the Earth radiates as much heat as it absorbs when its surface and atmosphere are as described by EA1. Because the Earth and its atmosphere radiate a total of of 252.5 W/m2, we suppose that a like amount of heat arrives from the Sun and lands upon the Earth's surface. When we place a 1-km layer of cloud in the way, we estimate that 10% of the Sun's heat will be reflected back out into space. When the cloud layer forms, the heat arriving from the Sun decreases to 227 W/m2 and the heat escaping from the Earth decreases to 136 W/m2.
By experimenting with TEP2, we find that a 13% increase in the absolute temperature of the Earth and its atmospheric layers will produce the following result.
------------------------------------------------The total escaping power is now 225 W/m2, which is close enough to the 227 W/m2 arriving from the Sun. When a cloud forms at altitude 10 km, the heat escaping from the Earth will balance that arriving from the Sun only if the Earth's surface warms by 38°C. If, instead of a cloud forming at 10 km, we double the CO2 concentration from 330 ppm to 660 ppm, the same calculation suggests the Earth will warm by only 1.5°C.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 327.7 653.9 629.9 0.0
0-km 316.4 568.3 413.4 0.0
3-km 305.1 491.3 284.7 0.0
6-km 282.5 361.1 169.3 0.0
9-km 259.9 258.7 250.4 201.4
12-km 248.6 216.6 34.6 14.8
15-km 248.6 216.6 23.5 8.7
------------------------------------------------
Total: 224.9
------------------------------------------------
According to our simulation, the formation of a 1-km thick layer of cloud at altitude 10 km has twenty-five times the warming effect as doubling the atmosphere's CO2 concentration.
UPDATE: Michele points out that high clouds will contain microscopic ice particles instead of water droplets. Ice, like water, is also opaque to long-wave radiation and transparent to short-wave radiation.
Thursday, October 14, 2010
Clouds
Clouds contain microscopic droplets of water. The droplets are around 10 μm in diameter and there are hundreds of them in every cubic centimeter (see here). We discussed the absorption of long-wave radiation by water in an earlier post. We presented a graph of water's absorption length versus radiation wavelength. The graph shows that the absorption length for 5 μm to 60 μm radiation is less than 20 μm. A 100-μm layer of water will absorb 99% of long-wave radiation.
Let us consider the fate of a single long-wave photon as it enters a cloud. The photon may pass all the way through the first centimeter of the cloud without touching a single droplet, or it might strike a droplet. If we assume our droplets have cross-section 100 μm2, the chance of our photon striking any particular droplet while passing through the first cubic centimeter is one in a million. The chance of the photon striking any one of a hundred droplets in the same cubic centimeter is a hundred times greater, or one in ten thousand. In every 100 m of cloud, the expected number of droplets our photon will strike is one (that's one in ten thousand per centimeter times ten thousand centimeters).
When the photon strikes a droplet, it can reflect off the surface or it can enter the liquid. According to this graph from Querry et al., the reflectance of water to long-wave radiation is 2% when the photon approaches at 10° to the perpendicular, 10% at 60°, 20% at 70° and 80% at 87°. The chance of a long-wave photon reflecting from a random spot on the surface of a droplet is around 10%. We also note that most reflection takes place when the photon strikes the droplet at a small angle to the surface, so the photon will continue into the cloud after reflection.
If a photon enters a 10-μm droplet, it will pass through something like 10 μm of water and strike the opposite, inner surface. Here it might reflect back into the droplet. But let's keep things simple: if the photon strikes a droplet, it will most likely enter the droplet, pass through 10 μm of water and keep going.
With 100 droplets in each cubic centimeter, our photon must pass through one droplet on average for each hundred meters of cloud. In 1 km of cloud, our photon will pass through ten droplets. In order to pass through the cloud, it will have to pass through roughly 100 μm of water. But we know that 100 μm of water absorbs 99% of all long-wave radiation. So a 1-km cloud is opaque to long-wave radiation.
Clouds have a different effect upon short-wave radiation, such as sunlight. Short-wave radiation reflects off the air-water surface far more readily than long-wave radiation, and once inside, it is more likely to reflect off the internal surface as well (internal reflection within droplets is what causes rainbows). But on the other hand, the absorption length of visible light in water is tens of meters. The water in a thick cloud will not absorb short-wave radiation. Instead, short-wave radiation changes direction as it encounters water droplets. It can change direction by reflecting off the outer or inner surface of a droplet. It can change direction by refraction as it enters or leaves a droplet. The reason thick clouds are dark is because sunlight is being turned around and re-directed back into space by the cloud's water droplets, not because sunlight is being absorbed by the clouds.
A short-wave photon passing through 1 km of cloud will encounter only ten droplets. These ten droplets are enough to absorb long-wave radiation, but they are not enough to guarantee that the short-wave photon gets re-directed back out of the cloud. With the help of some pencil drawings, we estimate that it would require encounters with one hundred droplets to guarantee that the photon came back out of the cloud on the same side that it went in. A 1-km thick cloud might reflect 10% of the short-wave radiation incident upon it, while a 10-km thick cloud will reflect 90%.
A 1-km layer of cloud acts like a black-body absorber of long-wave radiation. By radiative symmetry, this same 1-km layer must also be a perfect black-body radiator of long-wave radiation. We estimate that this same 1-km of cloud will allow 90% of short-wave radiation to pass through, while reflecting 10%. A 10-km layer of cloud, meanwhile, will allow only 10% of short-wave radiation to pass through, while reflecting 90%.
Heat radiated by the Earth will be absorbed by clouds. These same clouds will radiate their own heat out into space. Sunlight will be reflected off their top surfaces. In our next post, we will consider the effect of a 1-km layer of cloud at altitude 10 km upon the Earth's total escaping power and upon the amount of heat arriving from the Sun.
UPDATE: Cirrus clouds appear to be examples of our 1-km cloud layer. According to NASA, cirrus clouds are opaque to long-wave radiation, but largely transparent to short-wave radiation.
UPDATE: We see here confirmation of our estimates: clouds reflect from 10% to over 90% of short-wave radiation (albedo is 0.1 to over 0.9).
Let us consider the fate of a single long-wave photon as it enters a cloud. The photon may pass all the way through the first centimeter of the cloud without touching a single droplet, or it might strike a droplet. If we assume our droplets have cross-section 100 μm2, the chance of our photon striking any particular droplet while passing through the first cubic centimeter is one in a million. The chance of the photon striking any one of a hundred droplets in the same cubic centimeter is a hundred times greater, or one in ten thousand. In every 100 m of cloud, the expected number of droplets our photon will strike is one (that's one in ten thousand per centimeter times ten thousand centimeters).
When the photon strikes a droplet, it can reflect off the surface or it can enter the liquid. According to this graph from Querry et al., the reflectance of water to long-wave radiation is 2% when the photon approaches at 10° to the perpendicular, 10% at 60°, 20% at 70° and 80% at 87°. The chance of a long-wave photon reflecting from a random spot on the surface of a droplet is around 10%. We also note that most reflection takes place when the photon strikes the droplet at a small angle to the surface, so the photon will continue into the cloud after reflection.
If a photon enters a 10-μm droplet, it will pass through something like 10 μm of water and strike the opposite, inner surface. Here it might reflect back into the droplet. But let's keep things simple: if the photon strikes a droplet, it will most likely enter the droplet, pass through 10 μm of water and keep going.
With 100 droplets in each cubic centimeter, our photon must pass through one droplet on average for each hundred meters of cloud. In 1 km of cloud, our photon will pass through ten droplets. In order to pass through the cloud, it will have to pass through roughly 100 μm of water. But we know that 100 μm of water absorbs 99% of all long-wave radiation. So a 1-km cloud is opaque to long-wave radiation.
Clouds have a different effect upon short-wave radiation, such as sunlight. Short-wave radiation reflects off the air-water surface far more readily than long-wave radiation, and once inside, it is more likely to reflect off the internal surface as well (internal reflection within droplets is what causes rainbows). But on the other hand, the absorption length of visible light in water is tens of meters. The water in a thick cloud will not absorb short-wave radiation. Instead, short-wave radiation changes direction as it encounters water droplets. It can change direction by reflecting off the outer or inner surface of a droplet. It can change direction by refraction as it enters or leaves a droplet. The reason thick clouds are dark is because sunlight is being turned around and re-directed back into space by the cloud's water droplets, not because sunlight is being absorbed by the clouds.
A short-wave photon passing through 1 km of cloud will encounter only ten droplets. These ten droplets are enough to absorb long-wave radiation, but they are not enough to guarantee that the short-wave photon gets re-directed back out of the cloud. With the help of some pencil drawings, we estimate that it would require encounters with one hundred droplets to guarantee that the photon came back out of the cloud on the same side that it went in. A 1-km thick cloud might reflect 10% of the short-wave radiation incident upon it, while a 10-km thick cloud will reflect 90%.
A 1-km layer of cloud acts like a black-body absorber of long-wave radiation. By radiative symmetry, this same 1-km layer must also be a perfect black-body radiator of long-wave radiation. We estimate that this same 1-km of cloud will allow 90% of short-wave radiation to pass through, while reflecting 10%. A 10-km layer of cloud, meanwhile, will allow only 10% of short-wave radiation to pass through, while reflecting 90%.
Heat radiated by the Earth will be absorbed by clouds. These same clouds will radiate their own heat out into space. Sunlight will be reflected off their top surfaces. In our next post, we will consider the effect of a 1-km layer of cloud at altitude 10 km upon the Earth's total escaping power and upon the amount of heat arriving from the Sun.
UPDATE: Cirrus clouds appear to be examples of our 1-km cloud layer. According to NASA, cirrus clouds are opaque to long-wave radiation, but largely transparent to short-wave radiation.
UPDATE: We see here confirmation of our estimates: clouds reflect from 10% to over 90% of short-wave radiation (albedo is 0.1 to over 0.9).
Thursday, October 7, 2010
Absorption By All Higher Layers
Our Total Escaping Power program calculates the total power radiated by the Earth and its atmosphere given the absorption spectra of a sequence of atmospheric layers. The program does not dictate the thickness of these layers, nor even do the layers have to have the same thickness, but we did assume that radiation passing through one layer will be certain to pass through all higher layers. If we want to experiment with greater water vapor content in an upper layer, or if we want to include a layer of clouds, we will need a program that does not rely upon this assumption.
We modified our TEP1 program to produce TEP2. The new program applies the absorption of all higher layers to upward radiation. The result is a decrease in total escaping power. Here is the output of the new program when we apply it to our EA1 spectra, which assume 330 ppm CO2. We have added by hand a final column giving the change in escaping power caused by applying the absorption of all upper layers.
The enhancement of our model makes only a slight change in our CO2 doubling temperature, but it allows us to include upper layers that are more absorbent than lower layers. We can look forward to including layers of clouds and layers of excess humidity, and seeing how they effect the total escaping power.
We modified our TEP1 program to produce TEP2. The new program applies the absorption of all higher layers to upward radiation. The result is a decrease in total escaping power. Here is the output of the new program when we apply it to our EA1 spectra, which assume 330 ppm CO2. We have added by hand a final column giving the change in escaping power caused by applying the absorption of all upper layers.
---------------------------------------------------------In our discussion of TEP1, we claimed that our assumption of upper transparency would cause less than a 10% error in our calculation of total escaping power. It turns out that including the absorption of upper layers causes a 15% drop. Let's apply TEP1 to our EA2 spectra, which assume 660 ppm CO2.
Name Temp BB Layer Escaping Change
---------------------------------------------------------
Surface 290.0 401.1 388.8 80.0 -9.8
0-km 280.0 348.5 262.6 46.1 -12.8
3-km 270.0 301.3 184.8 39.7 -10.0
6-km 250.0 221.5 111.5 44.6 -6.8
9-km 230.0 158.7 50.7 26.4 -3.0
12-km 220.0 132.8 22.2 10.1 -1.1
15-km 220.0 132.8 14.4 5.5 -0.0
---------------------------------------------------------
Total: 252.5 -43.5
---------------------------------------------------------
------------------------------------------------We see a 5 W/m2 decrease in total escaping power due to doubling the CO2 concentration from 330 ppm to 660 ppm. The drop is 2.0%, slightly less than the 2.2% calculated by TEP1. If we repeat our calculation of CO2 doubling temperature using TEP2, we arrive at a value of 1.5°C, slightly less than the 1.6°C calculated by TEP1.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 290.0 401.1 388.8 78.8
0-km 280.0 348.5 264.0 44.2
3-km 270.0 301.3 188.6 38.2
6-km 250.0 221.5 115.2 43.9
9-km 230.0 158.7 53.4 26.4
12-km 220.0 132.8 24.2 10.3
15-km 220.0 132.8 16.3 5.7
------------------------------------------------
Total: 247.5
------------------------------------------------
The enhancement of our model makes only a slight change in our CO2 doubling temperature, but it allows us to include upper layers that are more absorbent than lower layers. We can look forward to including layers of clouds and layers of excess humidity, and seeing how they effect the total escaping power.
Wednesday, October 6, 2010
With 660 ppm CO2
In our In our previous post we extended our atmospheric absorption spectra to cover wavelengths 5 μm to 60 μm. These spectra assume CO2 concentration 330 ppm, which is typical for the Earth today, and temperature and water vapor concentration typical for a 30°N on a clear spring day. We plotted the extended spectra and applied them as input to our total escaping power program. The program says that the total power radiated by the Earth's surface and its atmosphere below the tropopause is 296.0 W.
Today we make one change to our atmospheric conditions: we double the CO2 concentration to 660 ppm. We leave water vapor concentration, temperature, and pressure the same. With the help of the Spectral Calculator, we obtain new absorption spectra and plot them.
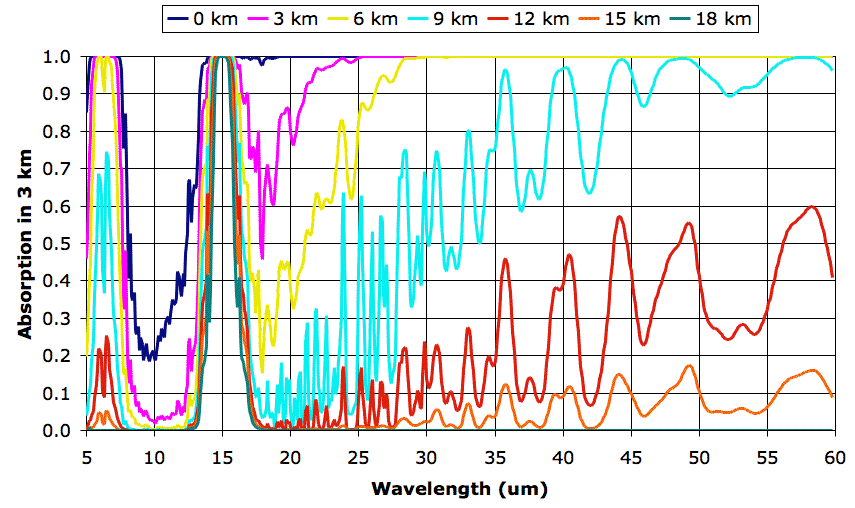
We feed our new spectra into our total escaping power program, and obtain the following output. The final column we added by hand. It gives us the change in total escaping power when we raise CO2 concentration from 330 ppm to 660 ppm.
According to Stephan's Law, the amount of power radiated by a black body increases as the fourth power of its temperature. For small changes in temperature, the amount of power radiated by any body will increase as the fourth power of its temperature. A 1% increase in temperature will cause a 4% increase in radiated power. In order to increase total escaping power by 2.2%, we can increase the temperature of the Earth's surface and all the atmospheric layers by one quarter of 2.2%, or 0.55%. We increased all our layer temperatures by 0.55% and applied our total escaping power program to the resulting atmospheric layers. We obtain the following output. Note that the new temperatures are recorded in the first column.
Our analysis considered only the heat radiated by the troposphere, which is the region of the atmosphere below the tropopause. We ignored the effect of increased CO2 upon the stratosphere, which is the region above the tropopause. Even though there is no net heat flow between the troposphere and the stratosphere, an overall warming or cooling of the stratosphere will affect the temperature of the troposphere, and therefore change its total radiated power. Furthermore, we ignored the effect of increased CO2 upon radiation arriving from the Sun. We will consider these effects in future posts. In our next post, however, we will try doubling the water vapor concentration in various atmospheric layers and re-calculating total escaping power. By this means, we will be able to determine whether the effect of CO2 upon total escaping power is significant compared that of water vapor.
UPDATE: See slightly improved calculation of CO2 warming in next post, where we arrive at 1.5°C instead of 1.6°C as the size of the effect.
Today we make one change to our atmospheric conditions: we double the CO2 concentration to 660 ppm. We leave water vapor concentration, temperature, and pressure the same. With the help of the Spectral Calculator, we obtain new absorption spectra and plot them.

We feed our new spectra into our total escaping power program, and obtain the following output. The final column we added by hand. It gives us the change in total escaping power when we raise CO2 concentration from 330 ppm to 660 ppm.
-------------------------------------------------------The total escaping power drops by 6.6 W/m2. The power escaping from the Earth's surface and the first three 3-km layers of the atmosphere decreases by 7.2 W/m2, but the power radiated by the top three layers increases by 0.8 W/m2. In the lower layers, more CO2 causes more radiation to be absorbed on its way into space. In the upper layers, more CO2 allows the atmosphere to radiate its heat more efficiently into space. We see that the increased absorption far outweighs the increased radiation, and the result is a 2.2% reduction in the heat escaping the Earth.
Name Temp BB Layer Escaping Change
-------------------------------------------------------
Surface 290.0 401.1 388.8 88.2 -1.6
0-km 280.0 348.5 264.0 55.6 -3.3
3-km 270.0 301.3 188.6 47.8 -1.9
6-km 250.0 221.5 115.2 51.0 -0.4
9-km 230.0 158.7 53.4 29.7 +0.3
12-km 220.0 132.8 24.2 11.5 +0.3
15-km 220.0 132.8 16.3 5.7 +0.2
-------------------------------------------------------
Total: 289.4 -6.6
-------------------------------------------------------
According to Stephan's Law, the amount of power radiated by a black body increases as the fourth power of its temperature. For small changes in temperature, the amount of power radiated by any body will increase as the fourth power of its temperature. A 1% increase in temperature will cause a 4% increase in radiated power. In order to increase total escaping power by 2.2%, we can increase the temperature of the Earth's surface and all the atmospheric layers by one quarter of 2.2%, or 0.55%. We increased all our layer temperatures by 0.55% and applied our total escaping power program to the resulting atmospheric layers. We obtain the following output. Note that the new temperatures are recorded in the first column.
------------------------------------------------We see that there is no net change in total radiated power when we combine a doubling of CO2 concentration with a 1.6°C warming of the Earth's surface. That's not to say that the Earth will actually warm up by 1.6°C if we double the CO2 concentration, because the climate might be a chaotic system that defies such simple logic, or a system with feedback that acts in quite the opposite manner to our expectations. Nevertheless, in the absence of such complex behavior, the doubling the CO2 concentration will tend to warm the Earth by 1.6°C. This 1.6°C is our estimate of the Earth's CO2 doubling temperature.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 291.6 410.0 397.5 90.6
0-km 281.5 356.1 269.3 57.0
3-km 271.5 308.1 192.3 48.8
6-km 251.4 226.5 117.4 52.0
9-km 231.3 162.3 54.4 30.2
12-km 221.2 135.8 24.7 11.7
15-km 221.2 135.8 16.7 5.9
------------------------------------------------
Total: 296.1
------------------------------------------------
Our analysis considered only the heat radiated by the troposphere, which is the region of the atmosphere below the tropopause. We ignored the effect of increased CO2 upon the stratosphere, which is the region above the tropopause. Even though there is no net heat flow between the troposphere and the stratosphere, an overall warming or cooling of the stratosphere will affect the temperature of the troposphere, and therefore change its total radiated power. Furthermore, we ignored the effect of increased CO2 upon radiation arriving from the Sun. We will consider these effects in future posts. In our next post, however, we will try doubling the water vapor concentration in various atmospheric layers and re-calculating total escaping power. By this means, we will be able to determine whether the effect of CO2 upon total escaping power is significant compared that of water vapor.
UPDATE: See slightly improved calculation of CO2 warming in next post, where we arrive at 1.5°C instead of 1.6°C as the size of the effect.
Subscribe to:
Comments (Atom)
