Random Fluctuations

In our previous post, Trends and Noise, we plotted the frequency spectrum of the global surface temperature for the past two hundred years and observed that it looks like red noise. Red noise is the noise we get when the change in a physical quantity from one sample to the next is random, instead of the deviation from some mean value being random. The graph below shows the year-to-year change in global surface temperature for the past two centuries.



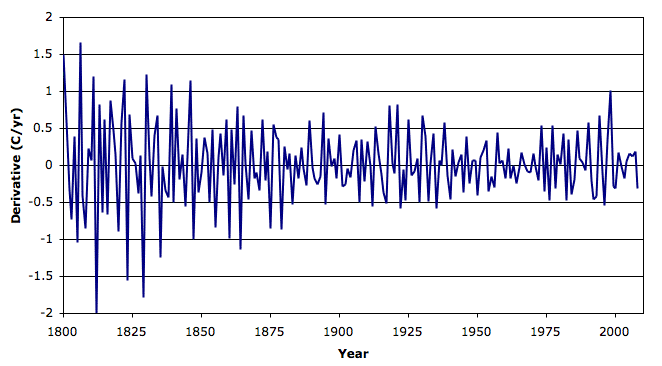
The distribution of these changes is not quite a normal distribution, but it's close. Its average value is 0.01°C for the entire period, and its standard deviation is 0.5°C. For period 1930−1990, its standard deviation is 0.3°C.



At the end of our essay on climate models, we suggest that a good model for the climate is a random change from one year to the next with normal distribution and standard deviation 0.3°C.

We challenged our readers to show that the climate is not dominated by random fluctuations. We posed the same question at Real Climate. We received three forms of answer. One was that the climate has been affected by volcanic eruptions and long-term solar cycles, therefore it is not random. Another was that we must assume things are not random, or else we can't believe in any scientific theory at all. Another was that experiments upon the climate are impractical (see this response from Gavin Schmidt), and because such experiments are impractical, climatologists should be excused from proving their theories with experiments.

We conclude that there is no empirical basis for a belief that recent climate trends are anything but random. Climatologists admit this lack of empirical basis openly, but insist that such a basis is not necessary to justify their belief in anthropomorphic global warming. What we have here is a disagreement about scientific method between those of us who work in physics and those who work in climatology.

UPDATE: Here is another red-noise analysis, shorter term, over at The Reference Frame.