Pressure Energy and Gravity

In our Circulating Cells program, we assume each cell has a uniform pressure. We know perfectly well, however, that the weight of the gas in the cell causes the pressure at the bottom to be greater than the pressure at the top. If p is the average pressure of the cell, m is the mass of the cell per square meter of its base area, and g is gravity, the pressure at the top will be p−mg/2 and at the bottom will be p+mg/2. Today we consider how our assumption of uniform pressure affects our calculation of cell enthalpy.



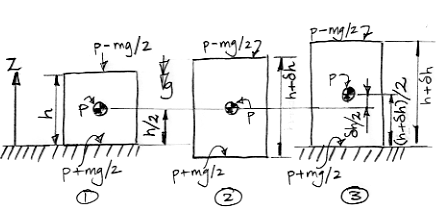
Our diagram shows a cell in three consecutive states. In state 1, the cell has height h and average pressure p. Its center of mass is at altitude h/2. In state 2, the cell has warmed up and expanded, but its center of mass remains at the same altitude. As the cell expanded, it pushed upwards with pressure p−mg/2 and downwards with pressure p+mg/2. The top and bottom surfaces each moved outwards a distance δh/2. The top surface does work work (p−mg/2)δh/2 and the bottom surface does work (p+mg/2)δh/2. The total work done by the gas as it expands is the sum of these two quantities, which comes out to be pδh. The mg terms cancel. Thus we get the same value for the total work done that we would obtain if we assumed a uniform pressure p pushing outwards for a total distance δh.

In state 3 we allow the cell to rise up, so that its bottom surface is once again sitting on the ground at altitude zero. The altitude of its center of mass is now (h+δh)/2. As the cell moved up, its height remained constant. Its top surface pushed upwards with force p−mg/2 over a distance δh/2. Meanwhile, something pushed upwards upon its bottom surface with force p+mg/2, and did so over the same distance. The top surface does work (p−mg/2)δh, but the bottom surface absorbs work (p+mg/2)δh. The net work done is upon the cell is mgδh. This time, the terms in p cancel and we are left with a term in mg. If we were to assume the pressure in the cell was uniform, we would not arrive at this same result. We would instead conclude that no net work was done upon the surfaces of the cell to raise them up.

We recall that the enthalpy of a cell is the work required to replace it with an identical cell from a reservoir. Because of the pressure difference across a cell, we see that the work we must do to raise a cell to altitude z is mgz, so we our calculation of enthalpy must include not only the pressure energy of the cell and its internal heat energy, but also a term mgz. This term has a name: it is the gravitational potential energy, which we add to the internal and pressure energy of a stationary cell to obtain its enthalpy per kilogram, H.

H = CvT + RT + gz = CpT + gz

The gas above our cell rises a total distance of δh, which requires work pδh per square meter of base area. We could say that the gravitational potential of the gas above our cell has increased by pδh, and we would be correct, but this increase is already accounted for in our enthalpy equation. The increase in our cell's pressure energy is RδT, where δT is the amount by which we warmed the cell to make it taller. For an ideal gas, RδT = pδh. Thus the increase in the pressure energy of our cell is one and the same as the increase in the gravitational potential energy of the gas pressing down upon it from above.

The gravitational potential term in our enthalpy equation represents the effect of the pressure drop across a cell as we change its altitude. By including the gravitational potential term, we can continue our enthalpy calculations with the assumption that the cell pressure is uniform. But an increase in gravitational potential is not accompanied by any change in the appearance or state of our cell. Gravitational potential is a useful and elegant concept, but it has no physical existence of its own.