Carbon Cycle: The Correlation Between Temperature and CO2

In our previous post we deduced from first principles a relationship between temperature and CO2 concentration in the atmosphere of our carbon cycle. In the appendices of this post, we show that our calculation is consistent with the van t'Hoff equation used by chemists to predict the concentration of CO2 above a water reservoir, and to measurements of the solubility of CO2 in water. In the main body of this post, we will see how our calculation compares to measurements of temperature and CO2 concentration in the Earth's atmosphere over the past half-million years.

In our carbon cycle equations, M_R is the mass of carbon in the oceanic reservoir, M_A is the mass of carbon in the atmosphere, k_R is the fraction of oceanic reservoir CO2 molecules that will be emitted into the atmosphere each year, and k_A is the fraction of atmospheric CO2 molecules that will be absorbed by the oceanic reservoir each year. The rate at which carbon is emitted by the oceanic reservoir is k_RM_R, and the rate at which it is absorbed by the oceanic reservoir is k_AM_A. At equilibrium, these two rates will be the same, so we have:

k_RM_R = k_AM_A      ⇒     M_A = k_RM_R/k_A      (Eq. 1)

In our previous post we concluded that k_A is constant with temperature, while k_R increases with temperature as e^−2300/T. Our consideration of the Earth's carbon-14 inventory showed that M_R = 77,000 Pg. In our natural, equilibrium carbon cycle, we found that M_A = 650 Pg. Given that the carbon must reside somewhere, even if M_A doubles or halves with temperature, M_R will change by less than 1%. So we can assume, to the first approximation, that M_R is constant with temperature. It is M_A that varies with temperature, and it does so in proportion to k_R.

M_A = k_RM_R/k_A ∝ e^−2300/T      (Eq.2)

Aa two temperatures T₁ and T₂, the equilibrium values of M_A, which we denote M_A(T₁) and M_A(T₂), are related by:

M_A(T₂) / M_A(T₁) = e^−2300/T₂ / e^−2300/T₁ = e^{2300(1/T₁−1/T₂)}      (Eq. 3)

Our (Eq. 3) predicts a close, positive correlation between temperature and atmospheric CO2 concentration, and it gives us an estimate of the magnitude of the change in CO2 concentration with temperature. The graph below shows atmospheric CO2 concentration provided by Barnola et al. and global temperature relative to today provided by Petit et al. over the past 425,000 years as determined from the Vostok ice cores.


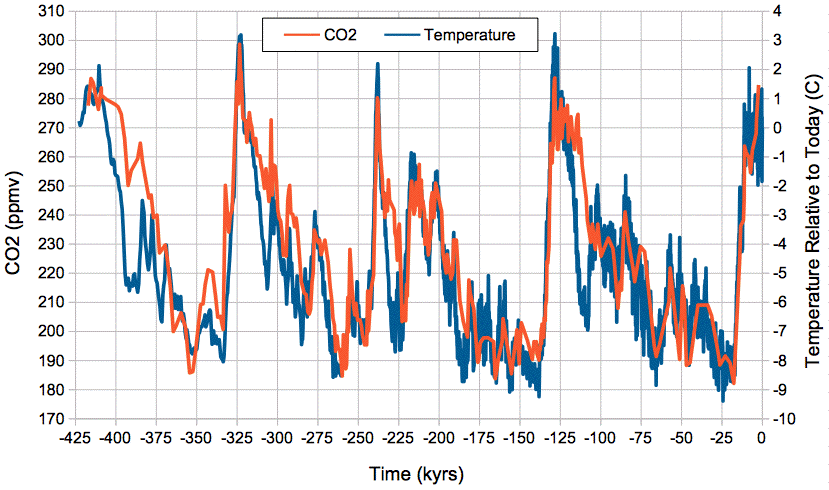
Figure: Absolute Atmospheric CO2 Concentration and Relative Temperature versus Time from Vostok ice cores. Click to enlarge. Local copies of data here and here.

We see close and sustained correlation between CO2 concentration and temperature, even as temperature varies by 12°C. If we assume today's average global temperature is 14°C = 287 K, the change from −9°C to +3°C relative to today is a swing from 278 K to 290 K. Our (Eq. 3) predicts an increase in the mass of carbon in the atmosphere by a factor of e^{2300(1/278−1/290)} = 1.41. Because almost all carbon in the atmosphere is bound up in CO2 molecules, the concentration of CO2 in the atmosphere is proportional to the total mass of carbon in the atmosphere, so when the total mass increases by a factor of 1.41, the CO2 concentration should increase by a factor of 1.41 also. Looking at the graph, we see CO2 rising from 190 ppmv to 290 ppmv, which is a factor of 1.52. Given the many uncertainties in our calculations, and in the ice-core measurements themselves, we are well-satisfied with the agreement between our calculations and the magnitude of the CO2 concentration changes in the ice core measurements.

We conclude that the correlation between CO2 concentration and temperature in the Earth's atmosphere over the past half million years is due to the effect of temperature upon the exchange of CO2 between the atmosphere and the oceanic reservoir of the Earth's carbon cycle. As the temperature rises, the CO2 concentration rises, and when temperature falls, the CO2 concentration falls.

Appendix 1: The van t'Hoff equation for CO2 and water states that the concentration of CO2 above the water is proportional to e^−2400/T. Our (Eq. 2) states that it is proportional to e^−2300/T. We are well-satisfied with this agreement.

Appendix 2: Suppose we have pure CO2 gas at atmospheric pressure above a reservoir of water. No matter how much CO2 the water dissolves, we maintain the same pressure of CO2 above the water. In this arrangement, unlike the arrangement of our carbon cycle, the concentration of CO2 in the water can vary. Applying the same reasoning we presented in our previous post, the rate at which CO2 molecules are absorbed by the water remains constant with temperature. At equilibrium, the rate at which CO2 molecules are emitted by the water must equal the rate at which they are absorbed, which means the rate of emission must also remain constant. But our calculation states that the probability of any given CO2 molecule in the water being emitted in a certain interval of time must increase with temperature as e^−2300/T. If the rate of emission is to remain constant, the concentration of CO2 in the water must decrease with temperature as e^2300/T. Only then will the rate of CO2 emission by the water, which is the product of the probability and the concentration, remain constant with temperature. We examine the plot of CO2 solubility in water versus temperature here. As temperature increases from 10°C to 20°C, the solubility of CO2 in water drops from 2.5 g/kg to 1.25 g/kg, which is a factor of 0.50. Our calculation suggests that it should drop by a factor of 0.58. We are well-satisfied with this agreement.