Carbon Cycle: Equations and Diagram

Suppose human beings start to add carbon to our natural, equilibrium atmosphere at a rate m_F by burning fossil fuels. We will express m_F in petagrams of carbon per year, or Pg/yr. Note that we have been working with carbon masses, not CO2 masses, but we can convert atmospheric carbon mass to atmospheric CO2 mass simply by multiplying by 3.7, which is the ratio of the molar mass of CO2 to the atomic mass of carbon-12. With the addition of m_F, our carbon cycle now looks like the diagram below. The time t = 0 yr is the moment just before we start we start adding m_F to the atmosphere.


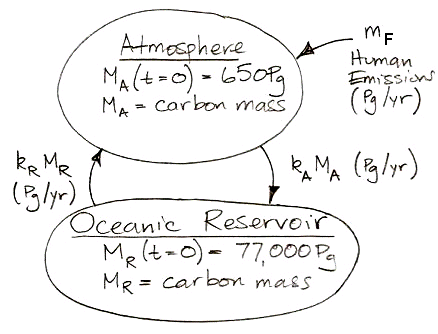
Or, expressed as two differential equations, it looks like this:


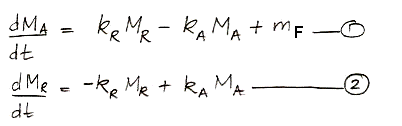
We can solve these differential equations in the same way we already solved those of carbon-14 concentration. Examining the equations, we see that we can obtain the behavior of non-radioactive carbon by setting the decay constant, γ, to zero and inserting the the human emission of carbon in place of the cosmic ray creation of carbon-14. More convenient than the analytic solution for our purposes, however, is a numerical solution that we can implement in a spreadsheet and combine with the historical and projected values for m_F as our study progresses.

In the numerical solution, we pick a time step small enough that changes in the masses and transfer rates are negligible during the step. Suppose our step is δt. Provided δt is small enough, we can assume, for example, that m_A during each step is equal to k_A times the value of M_A at the beginning of the step. We do not have to account for the fact that M_A may be changing during the step, because the time step is so small these changes will be negligible compared to M_A. For our carbon cycle, it turns out that one year is always a small enough time step, and in long, slow developments, ten years is small enough.

The following equations are the numerical equivalents of our differential equations. They show how we calculate M_A and M_R at time t+δt using their values at time t.


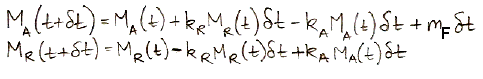
The current rate at which humans emit carbon by burning fossil fuels is close to, 10 Pg/yr. In our next post, we will set m_F to a constant 10 Pg/yr and calculate how our natural, equilibrium atmosphere responds over ten thousand years.

PS. If you find our carbon cycle drawing too confusing and drab, you can try this one drawn by my youngest son.