Carbon Cycle: Effect of Temperature

Up to now, we assumed that the temperature of our carbon cycle remained constant. We never specified what the temperature of the ocean or the atmosphere was. Nor did we assume that the temperature of the ocean or the atmosphere was uniform. We merely assumed that the temperature in each part of the system remained constant. Today we estimate how the rate of transfer coefficients of our carbon cycle, k_A and k_R, will change with temperature. We recall that k_A is the fraction of atmospheric CO2 molecules that will be absorbed by the oceanic reservoir each year, and k_R is the fraction of oceanic reservoir CO2 molecules that will be emitted into the atmosphere each year.

Claim: To the first approximation, k_A is independent of temperature.

Justification: Absorption of CO2 takes place at the surface of the ocean. The air pressure at sea-level is dictated by the weight of air per square meter pressing on the sea, which is roughly ten tonnes per square meter. When the atmosphere warms up, its mass does not change. The pressure at sea-level remains constant. But the air does expand. Because the air expands, the number of CO2 molecules per cubic meter decreases. Because the gas is warmer, each CO2 molecule is moving faster. Their average velocity is proportional to the square root of the absolute temperature. Suppose we increase the temperature from 14°C to 15°C. Absolute temperature increases from 287 K to 288 K. According to the gas law, the number of CO2 molecules per cubic meter at the ocean surface decreases by 0.35%. But their velocity increases by 0.18%, which means each CO2 molecule above the ocean surface collides with the ocean 0.18% more frequently than before. Combining these two effects, there will be a net 0.18% decrease in the number of opportunities for CO2 molecules to be absorbed. To the first approximation, this is no change at all. Let us also consider whether a faster-moving CO2 molecule, having collided with the ocean, is more or less likely to be absorbed. When CO2 dissolves in water, energy is released. The CO2 molecule does not need to supply any energy in order to be dissolved. A hotter CO2 molecule has more energy, but this energy is not required by dissolution, and will not make the reaction more likely. To the first approximation, therefore, a 1°C rise in temperature will have no significant effect upon k_A.

Claim: To the first approximation, K_R increases by a factor of 1.028 for each 1°C warming of the ocean surface.

Justification: Emission of CO2 takes place at the surface of the ocean. When the ocean warms by 1°C, its volume increases by 0.02%, which is insignificant. As we showed above, the warmer CO2 molecules will collide with the ocean surface 0.18% more often, but this, too, is insignificant. Let us consider whether a faster-moving CO2 molecule, having reached the surface of the ocean, is more or less likely to be emitted into the atmosphere. The emission of CO2 from solution requires heat. The enthalpy of dissolution for CO2 in water is −19.4 kJ/mole = −0.20 eV per CO2 molecule. (Compare to 0.42 eV latent heat of vaporization and −0.062 eV latent heat of fusion for an H20 molecule, and 0.26 eV latent heat of sublimation for a CO2 molecule.) Each CO2 molecule dissolving in water releases 0.20 eV of heat. Conversely, in order to be un-dissolved, a CO2 molecule needs to supply at least 0.20 eV from its own thermal energy. At 14°C, the average molecule has kinetic energy only 0.025 eV. But a tiny fraction will have, by random collisions, a much higher energy, as dictated by the Boltzmann distribution. In a given period of time, the number of molecules that attain energy E is proportional to e^−E/kT, where T is absolute temperature, k = 8.62×10⁻⁵ eV/K is the Boltzmann constant, and e = 2.72 is the exponential constant. The rate at which any reaction requiring thermal energy E takes place is proportional to e^−E/kT. Thus k_R is proportional to e^−E/kT, which means there is some constant, A, with units of 1/yr, for which k_R = A e^{−0.2/0.0000862T} = Ae^−2300/T. In our natural, equilibrium carbon cycle, k_R = 0.00048 1/yr. Suppose the natural, equilibrium temperature of the ocean surface is 14°C = 287 K. We can obtain the value of A as follows.

k_R @ 287K = Ae^−2300/287 = A×0.00033 = 0.00048 1/yr ⇒ A = 1.45 1/yr.

We raise the temperature by 1°C to 15°C = 288 K and re-calculate the rate.

k_R @ 288K = 1.45 e^−2300/288 = 0.000493 1/yr.

The rate has increased by a factor of 0.000493/0.00048 = 1.028, which is 2.8%. If we use 10°C or 20°C as our initial ocean temperature, we get 2.9% and 2.7% rises respectively. To the first approximation, each 1°C increase in temperature increases k_R by 2.8%, regardless of our guess at the initial temperature of the ocean surface.

We simulate the effect of a sudden 1°C warming of our carbon cycle in the following way. We begin with our natural, equilibrium atmosphere, described by our carbon cycle model. We increase k_R by 2.8%. We set the fossil fuel emission, m_F, to zero. We obtain the following plot of atmospheric CO2 concentration versus time.


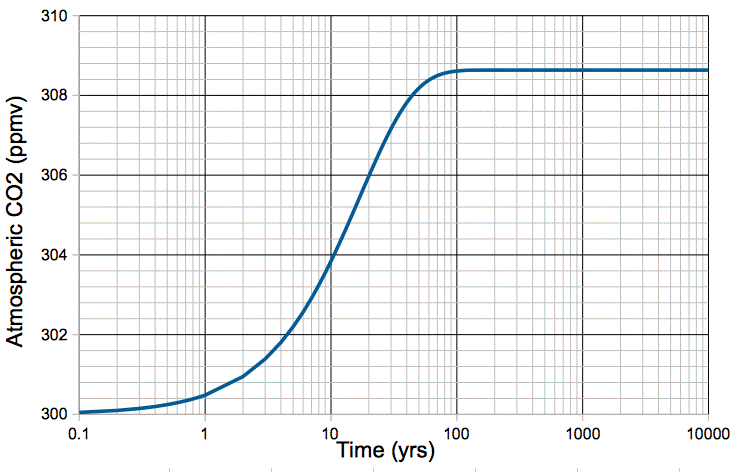
Figure: Atmospheric CO2 Concentration Following a 1°C Step Increase in Temperature.
The increase in temperature causes an immediate 2.8% increase in the rate at which CO2 is emitted by the ocean, but no increase in the rate at which it is absorbed. The additional CO2 released by the ocean builds up in the atmosphere. As the concentration of CO2 in the atmosphere increases, the rate at which it is absorbed by the ocean increases, because there are more CO2 molecules available for absorption. When the atmospheric concentration has increased by 2.8%, the rate of absorption is once again equal to the rate of emission. The carbon cycle reaches its new equilibrium in roughly one hundred years.

In our next post, we will see how well our calculations agree with the many empirical observations of carbon dioxide in solution, and with the history of our atmosphere over the past half-million years.