Carbon 14: Size of the Carbon Reservoir

Carbon-14 is produced at roughly 7.5 kg/yr in the atmosphere. Its atmospheric concentration is one part per trillion (1.0 ppt). Its half-life is 5700 years. These three observations imply the existence of the carbon cycle we described in our previous post. Our graphical representation of the carbon cycle uses the quantities listed in the table below. Together, these quantities provide a complete description of the cycle. Their numerical values apply to our natural, equilibrium atmosphere, which is based upon the Earth's atmosphere at the end of the nineteenth century. So far, we have values for all but two of these quantities: the mass of carbon in the reservoir, and the mass of carbon exchanged each year between the reservoir and the atmosphere.

Symbol	Quantity	Value
mpC14	production rate of carbon-14 in atmosphere	7.5 kg/yr
γ	decay rate of carbon-14	0.00012 kg/kg/yr
MA	mass of carbon in the atmosphere	650 Pg
CA	concentration of carbon-14 in atmosphere	1.0 ppt at equilibrium
MR	mass of carbon in the reservoir	unknown, Pg
me	exchange rate of CO2 between atmosphere and reservoir	unknown, Pg/yr
CR	concentration of carbon-14 in reservoir	0.8 ppt at equilibrium

Table: Carbon Cycle Quantities. We have 1 Pg = one petagram = 10¹² kg = 10¹⁵ g.
Another way to represent the carbon cycle is with two differential equations, as shown below, where d/dt represents the rate of change of a quantity with time, where t is time in years. Thus dC_A/dt is the rate of change of the concentration of carbon-14 in the atmosphere with time, in units of ppt/yr.


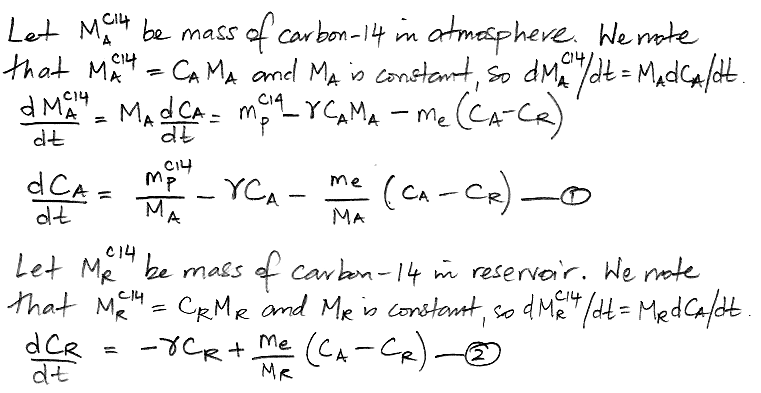
When our carbon cycle reaches equilibrium, the concentration of carbon-14 in the atmosphere and the reservoir settles to a constant value, so the d/dt terms are zero. This observation reduces our two differential equations to two simple algebraic equations, and we can solve for our two unknown quantities.


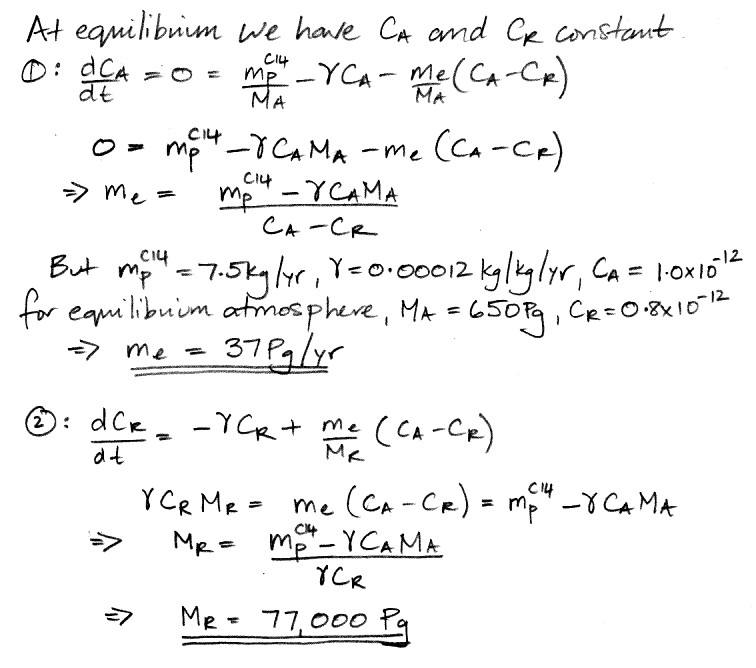
We have 37 Pg of carbon transported into the reservoir every year, including 37.0 kg of carbon-14 because the atmosphere's concentration of carbon-14 is 1.0 ppt. Another 37 Pg of carbon is emitted by the reservoir every year, including 29.6 kg of carbon-14 because the reservoir's concentration of carbon-14 is 0.8 ppt. The net flow of carbon-14 is 7.4 kg/yr into the reservoir (subtract 29.6 kg/yr from 37 kg/yr). The reservoir itself, meanwhile, contains 77,000 Pg of carbon, of which 62,000 kg is carbon-14. The reservoir's carbon-14 decays at 7.4 kg/yr (multiply 62,000 kg by 0.0012 kg/kg/yr ). As is required by the state of equilibrium, the net flow of carbon-14 into the reservoir each year is equal to the amount of carbon-14 that decays in the reservoir each year. We also have 0.1 kg of carbon-14 decaying in the atmosphere each year, so the total mass of carbon-14 that decays each year is 7.5 kg, which is equal to the amount that cosmic rays create, which is also required by the state of equilibrium.

Although our quantities deal only with masses of carbon, we note that all exchanges of carbon between the atmosphere and the reservoir take place in the form of exchanges of CO2. In particular, all carbon-14 in the atmosphere is bound up in CO2. We assumed earlier in our argument that the residence time of carbon carbon-14 in the atmosphere was much longer than the two months it takes for newly-created carbon-14 to react with oxygen to form CO2. We can now check the validity of this assumption: we have 650 Pg of carbon in the atmosphere, and 37 Pg of carbon flowing from the atmosphere into the reservoir each year. The residence time of a carbon-14 atom in the atmosphere is eighteen years (divide 650 Pg by 37 Pg/yr), which is much longer than two months, so our assumption turns out to be correct.

We conclude that our natural, equilibrium atmosphere exchanges 37 Pg of carbon each year with a reservoir that contains 77,000 Pg of carbon. Furthermore, because all carbon in the atmosphere is in the form of CO2, and all exchanges of carbon with the reservoir are in the form of CO2, the atmosphere exchanges 140 Pg of CO2 with the reservoir every year, and the reservoir itself contains 280,000 Pg CO2 (multiply by carbon mass by the molecular weight of CO2 and divide by the atomic weight of carbon). Meanwhile, the 650 Pg of atmospheric carbon is contained in 2,400 Pg of atmospheric CO2. That is to say: the carbon reservoir is a CO2 reservoir, and it contains more than a hundred times as much CO2 as the atmosphere.