Carbon-14: The Bomb Tests

Between the years 1945 and 1962, we detonated hundreds of atomic bombs in the atmosphere. Most of these, and certainly the largest, were detonated in the five years leading up to the Partial Test Ban Treaty in late 1963, which banned further atmospheric detonations. Atomic explosions produce carbon-14. By 1964, bomb tests had produced enough carbon-14 to double the atmospheric carbon-14 concentration. The graph below shows atmospheric carbon-14 concentration relative to its value before the bomb tests, as measured by various groups.


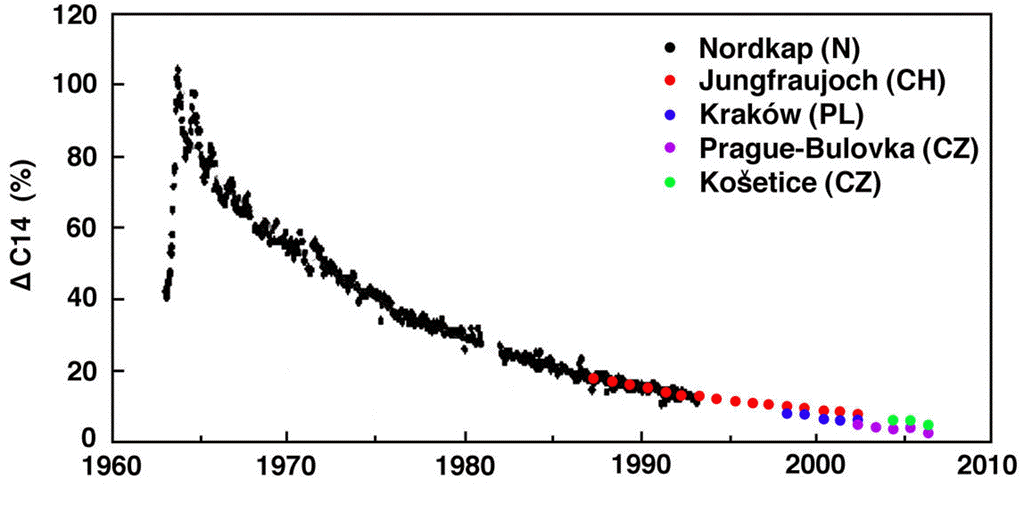
Figure: Atmospheric Concentration of Carbon-14 During and After the Bomb Tests. This graph is from an essay by Pettersson. The author combined measurements from several stations to produce the most complete graph we could find. For alternate plots, see here and here.
The relaxation of the atmospheric carbon-14 concentration from its peak follows an exponential decay with time constant roughly 15 years. After fifty years, the concentration is within a few percent of its value before the bomb tests. The carbon-14 did not linger in the atmosphere. It disappeared. Let's see if our model of the Earth's carbon cycle predicts this same relaxation or not.

In our model, carbon-14 concentrations are governed by two differential equations. We already solved these equations for a starting-point of zero in the atmosphere and the reservoir. Using the same procedure, we can solve the equations for a starting point of 2.0 ppt in the atmosphere and 0.8 ppt in the reservoir, which is the state the atmosphere was in at the time of the Partial Test Ban Treaty, when atmospheric tests were stopped. We obtain the following solutions for atmospheric concentration, C_A, and reservoir concentration C_R.

C_A = 1.0 + 0.987 e^−t/17 + 0.013 e^−t/8200
C_R = 0.8 + 0.0089 e^−t/17 − 0.0089 e^−t/8200

We note that this as t → ∞, we have C_A → 1.0 ppt and C_R → 0.8 ppt, as before. Whatever carbon-14 we add to the atmosphere, it will eventually decay, and we will be left once again with the concentrations generated by cosmic ray production. The above equations produce the graph of atmospheric and reservoir concentration shown below.


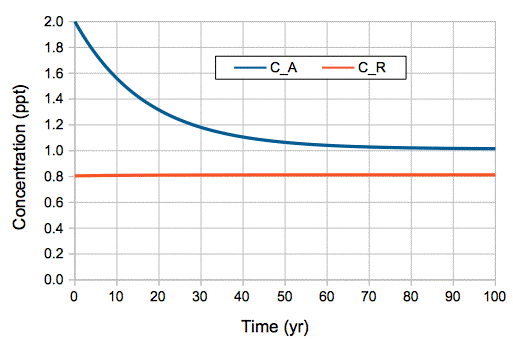
Figure: Carbon Cycle Model's Prediction of Atmospheric and Reservoir Carbon-14 Concentration After Sudden Doubling of Atmospheric Concentration.
Our simple, two-part, uniform-reservoir model of the carbon cycle predicts an exponential relaxation of carbon-14 concentration after the bomb tests, with a time constant of 17 years. Needless to say: agreement between the model and observation is superb.