Carbon-14: The Carbon Cycle

When a carbon-14 atom is created in the atmosphere by a cosmic ray, it quickly combines with oxygen to form carbon monoxide (CO). In a couple of months, this carbon monoxide combines with more oxygen to form radioactive carbon dioxide (CO2). As we showed previously, almost all carbon-14 created in the atmosphere ends up in a reservoir outside the atmosphere. But how long does the average carbon-14 atom spend in the atmosphere before it leaves? Our equilibrium atmosphere contains 650 kg of carbon-14, while 7.5 kg are created by cosmic rays every year. Almost one century's worth of carbon-14 production is stored in the atmosphere. It is most likely, therefore, that the averge carbon-14 atom spends several years in the atmosphere before it passes into the reservoir. Let us assume, for now, that the residence time of carbon-14 in the atmosphere is much longer than the two months it takes for carbon-14 to be bound up into a CO2 molecule. We will come back and check the validity of this assumption later. For now, we assume that all carbon-14 in the atmosphere is bound up in radioactive CO2.

The composition of the atmosphere is such that over 99.5% of its carbon is in the form of CO2. When we observe that one in a trillion carbon atoms is carbon-14, this is equivalent to saying that one in a trillion CO2 molecules is radioactive CO2. But radioactive CO2 is chemically identical to normal CO2. The extra two neutrons in its carbon nucleus have no effect upon its interactions with other molecules. When one molecule of radioactive CO2 leaves an atmosphere that contains 1 ppt (one part per trillion) of carbon-14, it does so in the company of one trillion normal CO2 molecules. When one carbon-14 atom leaves the atmosphere, it does so with one trillion other carbon atoms. The reservoir of carbon-14 that must exist outside the atmosphere must also be a much larger reservoir of normal carbon. The concentration of carbon-14 in this reservoir cannot be greater than in the atmosphere, because the atmosphere is where the carbon-14 is created. We already calculated that the reservoir contains 62 Mg of carbon-14, so it must also contain at least 62,000 Pg (sixty-two thousand Petagrams) of normal carbon (divide the mass of carbon-14 by the maximum possible concentration of carbon-14 in the reservoir). The reservoir contains one hundred times as much carbon as our equilibrium atmosphere.

In order for carbon-14 to leave the atmosphere, it must be carried by radioactive carbon dioxide, which in turn means that there must be a trillion times as much normal carbon dioxide leaving the atmosphere. But our equilibirum atmosphere is, by assumption, in in equilibrium. Its carbon dioxide content, and therefore its carbon content, is constant. If m_e kilograms of carbon leave the atmosphere every year and enter the reservoir, we must have the same m_e kilograms of carbon leaving the reservoir and entering the atmosphere every year. Thus the carbon content of the reservoir remains constant as well.

If the carbon-14 concentration of the reservoir were the same as the atmosphere's, we would have the same amount of carbon-14 leaving the atmosphere as returning, because the amount of normal carbon leaving is the same as the amount returning. Therefore, the concentration of carbon-14 in the reservoir must be lower than in the atmosphere. Let the concentration in the atmosphere be C_A and in the reservoir be C_R. The net flow of carbon-14 out of the atmosphere will be m_e(C_A−C_R), which we already calculated to be 7.4 kg/yr.

It remains for us to estimate the equilibrium concentration of carbon-14 in our carbon reservoir. It is well known that carbon is stored in vegetation and in the oceans. One kilogram of water at 14°C will hold around 0.5 g of carbon in the form of dissolved CO2. Given that the mass of the oean is roughly 1.4×10²¹ kg, the oceans have have the potential to store up to 700,000 Pg of carbon. The Earth's biomass, meanwhile, appears to contain only 2,000 Pg of carbon. So we will assume that the majority of the Earth's carbon reservoir is in the oceans. The concentration of carbon-14 in the deep oceans was measured by Bien et al. to be around 80% of the concentration in the atmosphere. So we will assume that the equilibrium concentration of carbon-14 in the Earth's carbon-14 reservoir is 0.8 ppt.

The diagram below illustrates what we have concluded so far about the exchange of carbon between the atmosphere and the reservoir. The masses of carbon in the atmosphere and the reservoir are M_A and M_R respectively. The decay rate of carbon-14 is γ.


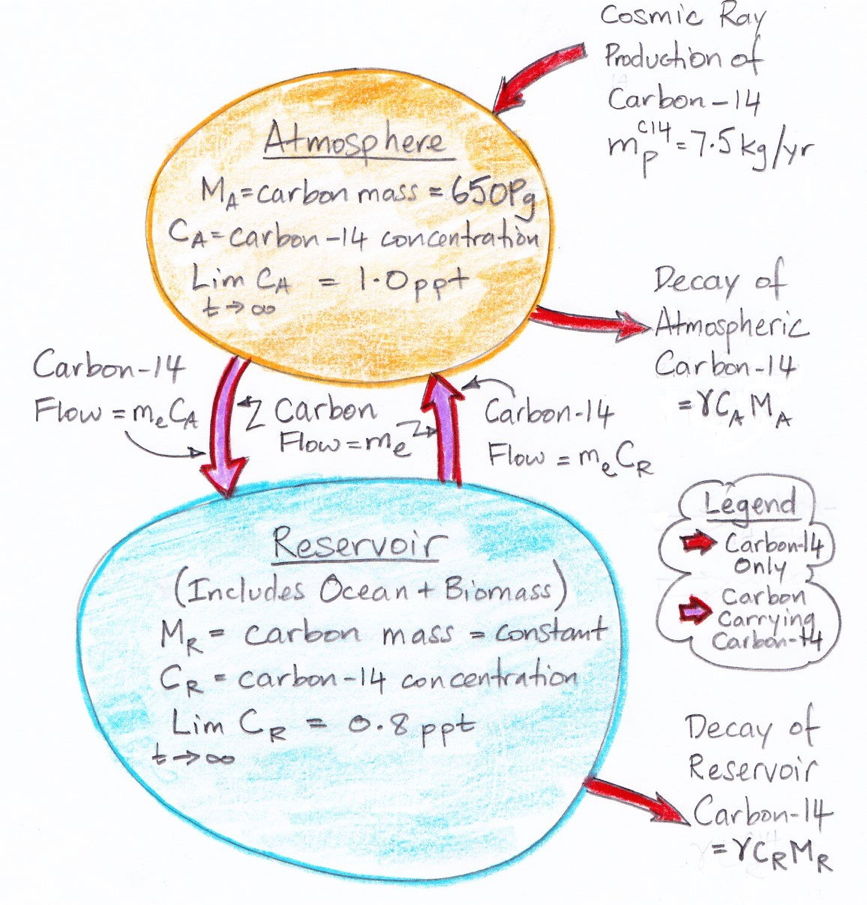
The diagram assumes that the carbon exchange between the atmosphere and the reservoir has already reached equilibrium. But it does not assume that the carbon-14 concentration has reached equilibrium. We are going to obtain an analytic solution for the evolution of carbon-14 concentration from a starting point of no carbon-14 at all. So instead of pre-supposing that we have already reached carbon-14 equilibrium, the diagram states that, given infinite time, the carbon-14 concentration in the atmosphere and reservoir will eventually reach equilibrium at 1.0 and 0.8 ppt respectively.

What is expressed in the diagram we can write down in two differential equations with some boundary conditions. The two equations contain two unknown constants: the carbon exchange rate, m_e, and the size of the carbon reservoir, M_R. In our next post, we will use these two differential equations to deduce the values of m_e and M_R.