The Fourth 3-km Layer

The following graph shows the absorption of long-wave radiation by the fourth 3-km layer of the Earth's atmosphere, from altitude 9 km to 12 km. This line is the same as the 9-km line in our Earth's Atmosphere post. The absorption is typical of a clear day in April, at latitude 30° North. Water vapor content is only 100 ppm (that's 0.01%), which is one tenth the concentration present in the third 3-km layer, just below. Air pressure is 410 mbar and temperature is 230 K (that's −43°C). We have CO2 present in 330 ppm, just as in the earlier layers.



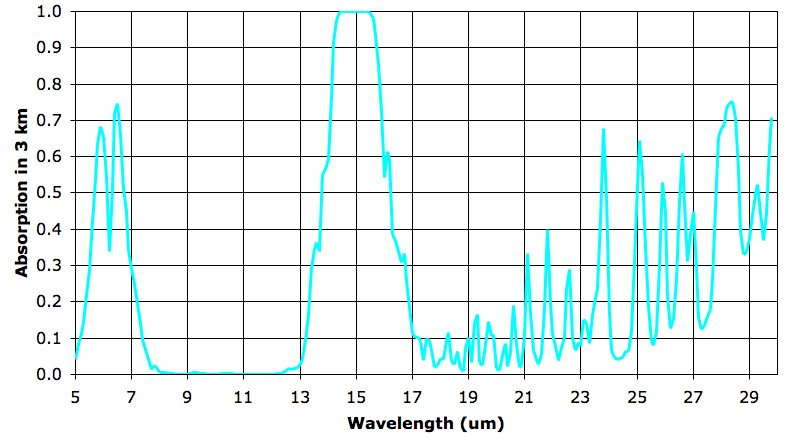
As before, we simplify our analysis of the absorption spectrum by saying that our 3-km layer is transparent when it absorbs less than 63% of a wavelength and opaque otherwise. The fourth 3-km layer is transparent from 5.0 to 14.1 μm, with the exception of a couple of narrow bands around 6 μm which we will ignore for the sake of simplicity. The fourth layer is again transparent from 15.9 to roughly 28 μm.

The biggest change between the third and fourth layers is the new transparency from 5.4 to 7.3 μm. In the third 3-km layer, water vapor was still absorbing at these wavelengths, but now the water vapor is so sparse that it becomes transparent. Radiation by water vapor in the third 3-km layer at these wavelengths will pass through the fourth and higher layers, and so out into space. We also see an end to the absorption by water vapor for the range 23 to 28 μm.

Another thing that is striking about the fourth 3-km layer is how clearly the absorption by CO2 stands out and remains strong. Let us apply our opaque-transparent simplification to the absorption of the third and fourth layers to estimate how CO2 affects radiation into space by the third 3-km layer. In the third layer, CO2 was opaque from 13.8 to 16.2 μm. In this layer it is opaque from 14.1 to 15.9 μm.

To the first approximation (we split the atmosphere into layers and we assume the atmosphere is either opaque or transparent but never half-way between), 80% of the upward-going radiation emitted by the CO2 in the third layer will be absorbed by the CO2 in the fourth layer, and 100% of the downward-going radiation emitted by the CO2 in the fourth layer will be absorbed by the CO2 in the third layer.