Cosmic rays turn roughly 7.5 kg of atmospheric nitrogen into carbon-14 every year. Carbon-14 decays at 0.00012 kg/kg/yr. There must be 62,500 kg of carbon-14 on Earth, because 62,000 kg decays at 7.5 kg/yr. At the end of the nineteenth century, the atmosphere contained 300 ppmv CO2, or 650 Pg of carbon, of which 1 ppt was carbon-14, or 650 kg. Roughly 0.1 kg/yr of this 650 kg decayed each year, but the remaining 7.4 kg/yr had to leave the atmosphere somehow, entering some kind of carbon-14 reservoir.
This reservoir would have to contain the remaining 62,000 kg of carbon-14 we know must exist on Earth. Given that carbon-14 is chemically identical to normal carbon, the passage of one carbon-14 atom into the reservoir implies without any ambiguity that one trillion normal carbon atoms enter at the same time. Because carbon-14 is created in the atmosphere, the concentration in the reservoir could not be greater than 1.0 ppt, which means the reservoir would have to contain at least 62,000 Pg of carbon in order for it to hold 62,000 kg of carbon-14.
These observations are all unassailable facts of nineteenth century Earth, and indeed of Earth today. All of the quantities we have listed remain the same to within 10%, with the exception of the CO2 concentration, which has risen by 30%. We still cannot escape the conclusion that there exists a carbon reservoir on Earth of at least 60,000 Pg that is in ready communication with the atmosphere.
Having advanced the above argument in detail, we made two assumptions about the carbon cycle in order to develop a simple model of its behavior. We assumed that the carbon-14 concentration in the reservoir was uniform, and we assumed that this concentration was 0.8 ppt, which is the concentration in the deep oceans. With these assumptions we obtained two differential equations describing the carbon-14 concentration in the Earth's carbon cycle. The equations contained two unknown quantities: the mass exchange rate between the atmosphere and the reservoir, and the total size of the reservoir. In order to make the model fit our observed atmospheric concentration and our assumed reservoir concentration, we determined that the mass exchange rate had to be 37 Pg/yr and the reservoir had to contain 77,000 Pg of carbon.
Our one-reservoir, uniform-concentration model is already fully constrained by our observations of carbon-14 and the atmosphere. No adjustment to any of its parameters is possible without compromising its accuracy. The model predicts how the carbon-14 concentrations will respond to any change we care to imagine. In our previous post, we presented this plot of how the model predicts the concentrations will develop from a starting point of zero.
But how are we to know if these predictions are correct? What we have done so far is akin to plotting two observations on a graph, drawing a straight line through both, and declaring the straight line to be the place where all future observations will lie. It is true that there is only one straight line that we can draw through two points, but it is also true that we can draw a straight line through any two points. It is only when we have three or more points lying on the same straight line that a straight-line model becomes convincing. In the case of our model, we can always pick a value of mass exchange and reservoir size to make it fit our observations. If we are to have more confidence in our model, we must test it against other, independent observations of carbon-14 concentration. Until then, our model is merely a credible hypothesis: worth thinking about, but not conclusive.
This inconclusive position was the one Arnold et al. found themselves in when they published their study of the carbon cycle in 1956. They did the same analysis we have done, and they studied two-reservoir and three-reservoir models as well. The more complex models produced almost identical predictions to the one-reservoir model, so they concluded that the one-reservoir model was good enough. But they were unable to test the one-reservoir model with an independent observation of carbon-14 behavior in the atmosphere. No such observations existed at the time.
Now, sixty years later, we have the observations we need to test our carbon cycle model. In the 1960s, we inadvertently performed an experiment on the entire atmosphere, in which we doubled the mass of carbon-14 it contained. Our model makes a clear and unambiguous prediction of what will happen after such an event. If this prediction is inaccurate, our model must wrong. But if the prediction is accurate, the model must be reliable, because the chance of the model being accurate by chance is close to zero.
Saturday, October 31, 2015
Tuesday, October 27, 2015
Carbon-14: Establishing Equilibrium
We have so far assumed that one million years is sufficient time for the carbon-14 concentrations in our carbon cycle to reach their equilibrium values. That is to say: if we started with no carbon-14 in our carbon cycle, and cosmic rays added 7.5 kg/yr to the atmosphere, it would take less than one million years for the carbon-14 concentration to stabilize at 1.0 ppt in the atmosphere and 0.8 ppt in the reservoir. In our previous post, we obtained the following equations for atmospheric carbon-14 concentration, CA, and reservoir concentration, CR, starting from CA = CR = 0.0 ppt at time t = 0 yr. The equations assume units of ppt for concentration and years for time.
CA = 1.0 − 0.2 e−t/17 − 0.8 e−t/8200
CR = 0.8 + 0.002 e−t/17 − 0.802 e−t/8200
The figure below shows how the two concentrations increase with time. The scale is logarithmic, which allows us to see changes in the first year as well as in the final ninety thousand years.

After ten years, the atmospheric concentration has risen to 0.1 ppt. We have 65 kg of carbon-14 in the atmosphere, which is most of the 75 kg created by cosmic rays in ten years. The concentration in the reservoir remains close to zero (0.0002 ppt).
After one hundred years, the atmospheric concentration has settled upon a value of 0.2 ppt. The concentration in the reservoir remains close to zero (0.009 ppt). Cosmic rays have made 750 kg of carbon-14, but only 130 kg of this remains in the atmosphere. The exchange of 37 Pg/yr of carbon between the atmosphere and the reservoir is carrying 37 Pg/yr × 0.2 ppt = 7.4 kg/yr of carbon-14 from the atmosphere into the reservoir. This state of affairs continues through the first millennium: carbon-14 created by cosmic rays flows directly into the reservoir, with no significant amount of carbon-14 being carried back out again, because the concentration in the reservoir is still close to zero.
After a thousand years, the concentration in the reservoir has risen to 0.1 ppt. The reservoir is beginning to fill up. The concentration in the atmosphere is now 0.3 ppt. We note that 0.3 ppt is still 0.2 ppt higher than in the reservoir. The net flow of carbon-14 into the reservoir remains 7.4 kg/yr.
After ten thousand years, the reservoir concentration is close to 0.6 ppt. In the atmosphere it is close to 0.8 ppt. We still have a net flow of 7.4 kg/yr of carbon-14 into the reservoir each year, but now this 7.4 kg/yr is the difference between 28.7 kg/yr flowing into the reservoir and 21.3 kg/yr flowing out. At the same time, the growth in the reservoir concentration begins to slow. The rate at which carbon-14 is decaying in the reservoir is starting to be significant compared to the rate at which carbon-14 is being added to the reservoir. The reservoir now contains 45,000 kg of carbon-14, and it decays at 5.4 kg/yr.
After fifty thousand years, the concentrations have stabilized at 0.8 ppt in the reservoir and 1.0 ppt in the atmosphere. The difference is what is required to transport almost all carbon-14 created by cosmic rays into the reservoir. The reservoir now contains so much carbon-14 that the radioactive isotope decays into nitrogen at the same rate that carbon-14 is added from the atmosphere.
The time it takes to arrive at equilibrium is far shorter than one million years. Our model indicates that the concentration of carbon-14 in the reservoir will be set by the average carbon-14 creation rate over the past fifty thousand years. The concentration in the atmosphere, on the other hand, is the sum of the reservoir concentration and an increment that is proportional to the creation rate that has prevailed for the past fifty years. If cosmic rays were to stop suddenly, the carbon-14 concentration would drop to the reservoir concentration of 0.8 ppt within fifty years, and stay at 0.8 ppt for a thousand years before the drop in reservoir concentration became significant. Conversely, if cosmic rays were to double the rate of carbon-14 creation, the concentration in the atmosphere would rise to 1.2 ppt within fifty years, and stay at 1.2 ppt for almost a thousand years before the rise in reservoir concentration became significant.
CA = 1.0 − 0.2 e−t/17 − 0.8 e−t/8200
CR = 0.8 + 0.002 e−t/17 − 0.802 e−t/8200
The figure below shows how the two concentrations increase with time. The scale is logarithmic, which allows us to see changes in the first year as well as in the final ninety thousand years.

After ten years, the atmospheric concentration has risen to 0.1 ppt. We have 65 kg of carbon-14 in the atmosphere, which is most of the 75 kg created by cosmic rays in ten years. The concentration in the reservoir remains close to zero (0.0002 ppt).
After one hundred years, the atmospheric concentration has settled upon a value of 0.2 ppt. The concentration in the reservoir remains close to zero (0.009 ppt). Cosmic rays have made 750 kg of carbon-14, but only 130 kg of this remains in the atmosphere. The exchange of 37 Pg/yr of carbon between the atmosphere and the reservoir is carrying 37 Pg/yr × 0.2 ppt = 7.4 kg/yr of carbon-14 from the atmosphere into the reservoir. This state of affairs continues through the first millennium: carbon-14 created by cosmic rays flows directly into the reservoir, with no significant amount of carbon-14 being carried back out again, because the concentration in the reservoir is still close to zero.
After a thousand years, the concentration in the reservoir has risen to 0.1 ppt. The reservoir is beginning to fill up. The concentration in the atmosphere is now 0.3 ppt. We note that 0.3 ppt is still 0.2 ppt higher than in the reservoir. The net flow of carbon-14 into the reservoir remains 7.4 kg/yr.
After ten thousand years, the reservoir concentration is close to 0.6 ppt. In the atmosphere it is close to 0.8 ppt. We still have a net flow of 7.4 kg/yr of carbon-14 into the reservoir each year, but now this 7.4 kg/yr is the difference between 28.7 kg/yr flowing into the reservoir and 21.3 kg/yr flowing out. At the same time, the growth in the reservoir concentration begins to slow. The rate at which carbon-14 is decaying in the reservoir is starting to be significant compared to the rate at which carbon-14 is being added to the reservoir. The reservoir now contains 45,000 kg of carbon-14, and it decays at 5.4 kg/yr.
After fifty thousand years, the concentrations have stabilized at 0.8 ppt in the reservoir and 1.0 ppt in the atmosphere. The difference is what is required to transport almost all carbon-14 created by cosmic rays into the reservoir. The reservoir now contains so much carbon-14 that the radioactive isotope decays into nitrogen at the same rate that carbon-14 is added from the atmosphere.
The time it takes to arrive at equilibrium is far shorter than one million years. Our model indicates that the concentration of carbon-14 in the reservoir will be set by the average carbon-14 creation rate over the past fifty thousand years. The concentration in the atmosphere, on the other hand, is the sum of the reservoir concentration and an increment that is proportional to the creation rate that has prevailed for the past fifty years. If cosmic rays were to stop suddenly, the carbon-14 concentration would drop to the reservoir concentration of 0.8 ppt within fifty years, and stay at 0.8 ppt for a thousand years before the drop in reservoir concentration became significant. Conversely, if cosmic rays were to double the rate of carbon-14 creation, the concentration in the atmosphere would rise to 1.2 ppt within fifty years, and stay at 1.2 ppt for almost a thousand years before the rise in reservoir concentration became significant.
Saturday, October 24, 2015
Carbon-14: Analytic Solution to Concentration Equations
We can describe the origin and fate of carbon-14 with a diagram or a pair of differential equations. One of the assumptions upon which we have based our reasoning so far is that one million years is more than enough for carbon-14 concentrations to reach equilibrium. Today we solve the two differential equations with a starting point of 0.0 ppt carbon-14 in the reservoir and the atmosphere. Our solution will tell us how long it takes for equilibrium concentrations to be established. For those of you who are not interested in following the derivation, we invite you to await our next post, in which we use the solution to plot graphs of carbon-14 concentration versus time.
We begin by referring to our equations (1) and (2) as shown here. We re-arrange the equations so that all terms in CA are on the left side of (1) and all terms in CR are on the left side of (2). In doing so, we treat d/dt as if it were just another factor, which may seem odd, but it's accurate.
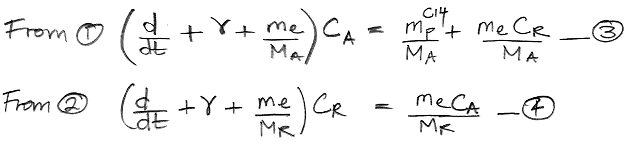
The only variables in these two equations are CA, CR, and time, t. All other parameters are constants that we have already calculated. We must eliminate CR from the (3) so as to obtain an equation in CA and t alone, which we can then solve. We eliminate CR by multiplying (3) by the same factor that we observe on the left side of (4).
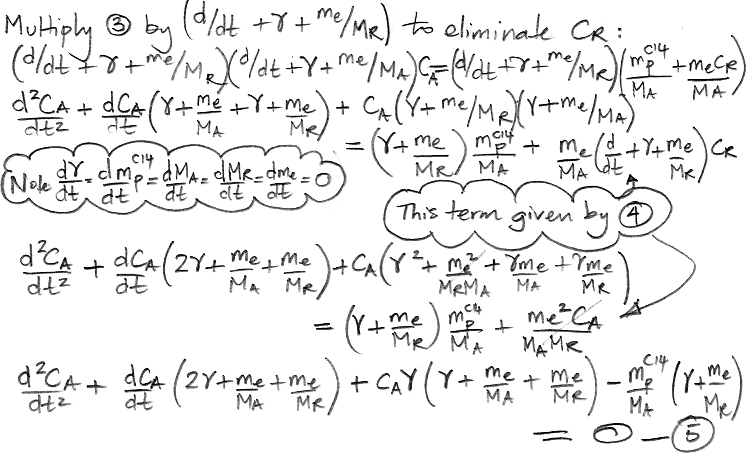
We do the same thing for CR, arriving at a differential equation in only CR and t.
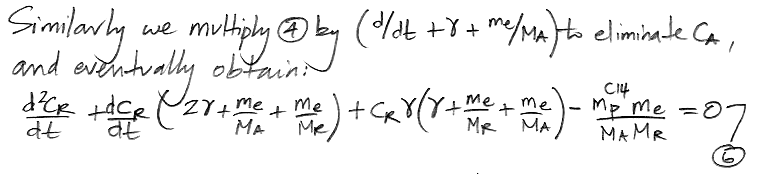
At this point we pause to check the equations by considering how they behave as time approaches infinity, as shown here, and we find that they appear to behave correctly. Both equations have solutions of the same form: a constant plus two decay terms.
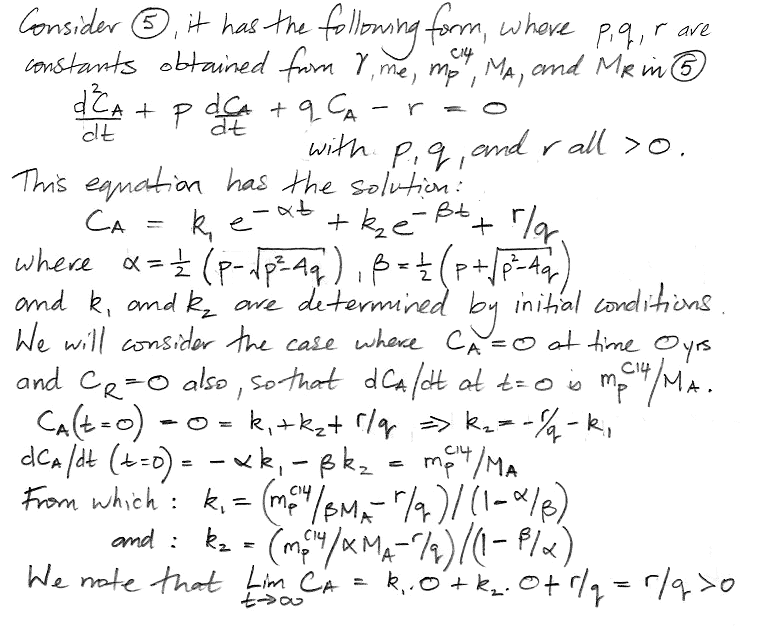
We insert values for mpC14, γ, MA, MR, and me and obtain values for all five constants in our solution. The coefficients α and β dictate how rapidly the concentration evolves with time. We have α = 0.0574 and β = 0.000122. We see that α is close to the fraction of the atmospheric carbon that is exchanged with the reservoir every year, while β is close to the decay rate of carbon-14. We have 1/α = 17 yr, which is the time constant of exchanges between the atmosphere and the reservoir, and 1/β = 8,200 yrs, which is the time constant of accumulation of carbon-14 in the reservoir. The weighting factors k1 and k2 are −0.2 and −0.8 respectively. Together, they add up to −1.0 ppt. The constant term is the equilibrium value of CA, which comes out as 1.0 ppt, which is what we expect, because we chose the value of me and MR to make sure that the equilibrium concentration would be 1.0 ppt. Our equation for CA is as follows, where concentration is in ppt and time is in years.
CA = 1.0 − 0.2 e−t/17 − 0.8 e−t/8200.
At t = 0, we have CA = 0 ppt, and when t→∞, CA→1.0 ppt, as we expect. The 17-yr decay term represents the flow of carbon-14 into the reservoir. The 8200-yr term represents the accumulation of carbon-14 in the reservoir. We obtain a similar solution for CR.
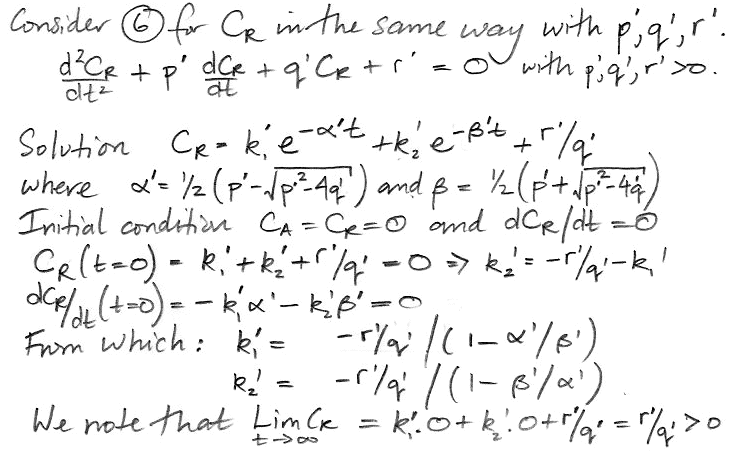
The coefficients α' and β' are the same as α and β. But the weighting factors are different, as is the constant term. Our equation for CR is,
CR = 0.8 + 0.002 e−t/17 − 0.802 e−t/8200.
At t = 0, we have CR = 0 ppt, and dCR/dt = k1α+k2β = 0.0 ppt/yr, and d2CR/dt2 = k1α2+k2β2 > 0, all of which we expect, and also when t→∞, we have CR→0.8 ppt, which is one of our starting assumptions.
We are pleased to have an analytic solution for CA and CR. A numerical solution to the differential equations turns out to be unstable for time steps greater than ten years. We want to plot CA and CR over a hundred thousand years. Ten thousand steps are cumbersome in a spreadsheet. Furthermore, the analytic solution us gives more insight into the way the parameters of the carbon cycle interact to govern its behavior.
We begin by referring to our equations (1) and (2) as shown here. We re-arrange the equations so that all terms in CA are on the left side of (1) and all terms in CR are on the left side of (2). In doing so, we treat d/dt as if it were just another factor, which may seem odd, but it's accurate.
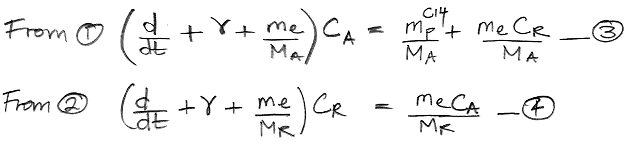
The only variables in these two equations are CA, CR, and time, t. All other parameters are constants that we have already calculated. We must eliminate CR from the (3) so as to obtain an equation in CA and t alone, which we can then solve. We eliminate CR by multiplying (3) by the same factor that we observe on the left side of (4).
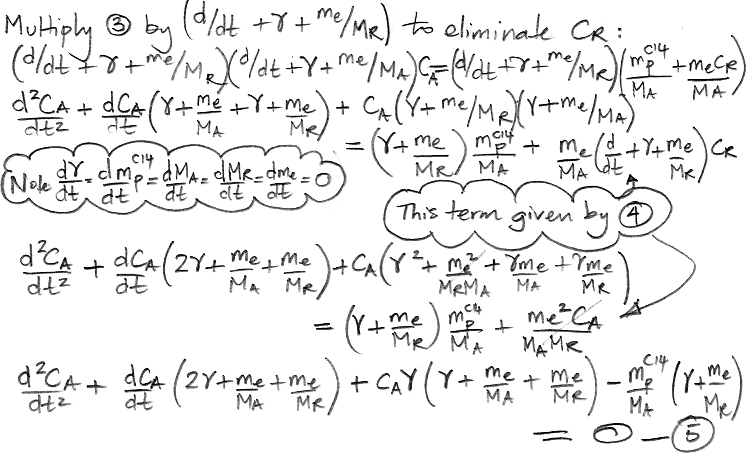
We do the same thing for CR, arriving at a differential equation in only CR and t.
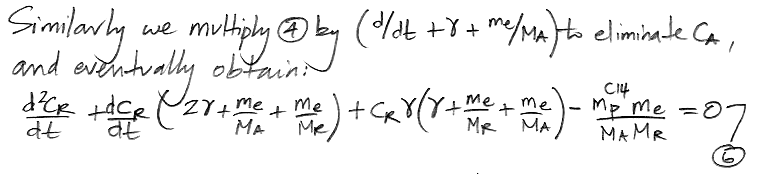
At this point we pause to check the equations by considering how they behave as time approaches infinity, as shown here, and we find that they appear to behave correctly. Both equations have solutions of the same form: a constant plus two decay terms.
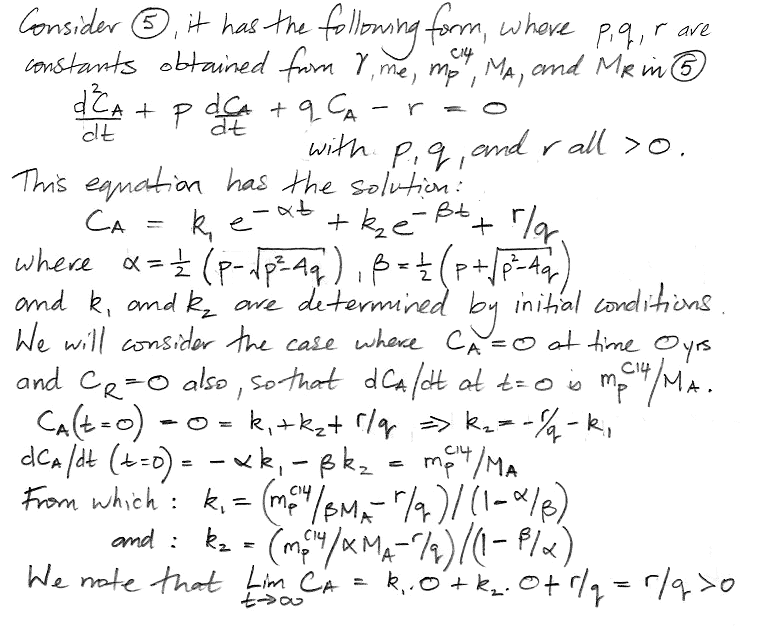
We insert values for mpC14, γ, MA, MR, and me and obtain values for all five constants in our solution. The coefficients α and β dictate how rapidly the concentration evolves with time. We have α = 0.0574 and β = 0.000122. We see that α is close to the fraction of the atmospheric carbon that is exchanged with the reservoir every year, while β is close to the decay rate of carbon-14. We have 1/α = 17 yr, which is the time constant of exchanges between the atmosphere and the reservoir, and 1/β = 8,200 yrs, which is the time constant of accumulation of carbon-14 in the reservoir. The weighting factors k1 and k2 are −0.2 and −0.8 respectively. Together, they add up to −1.0 ppt. The constant term is the equilibrium value of CA, which comes out as 1.0 ppt, which is what we expect, because we chose the value of me and MR to make sure that the equilibrium concentration would be 1.0 ppt. Our equation for CA is as follows, where concentration is in ppt and time is in years.
CA = 1.0 − 0.2 e−t/17 − 0.8 e−t/8200.
At t = 0, we have CA = 0 ppt, and when t→∞, CA→1.0 ppt, as we expect. The 17-yr decay term represents the flow of carbon-14 into the reservoir. The 8200-yr term represents the accumulation of carbon-14 in the reservoir. We obtain a similar solution for CR.
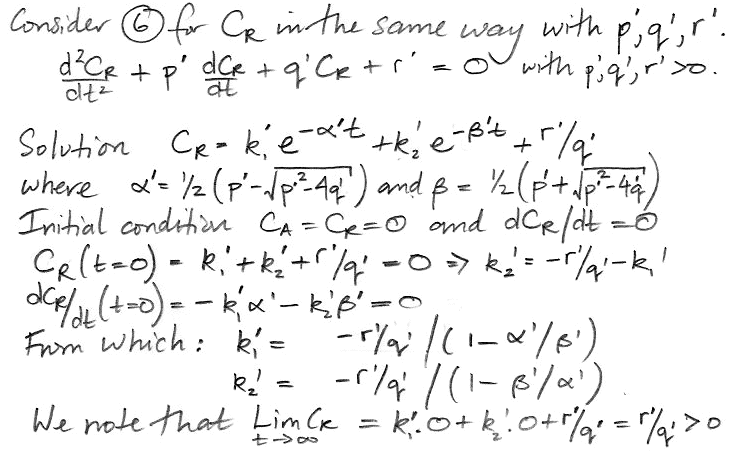
The coefficients α' and β' are the same as α and β. But the weighting factors are different, as is the constant term. Our equation for CR is,
CR = 0.8 + 0.002 e−t/17 − 0.802 e−t/8200.
At t = 0, we have CR = 0 ppt, and dCR/dt = k1α+k2β = 0.0 ppt/yr, and d2CR/dt2 = k1α2+k2β2 > 0, all of which we expect, and also when t→∞, we have CR→0.8 ppt, which is one of our starting assumptions.
We are pleased to have an analytic solution for CA and CR. A numerical solution to the differential equations turns out to be unstable for time steps greater than ten years. We want to plot CA and CR over a hundred thousand years. Ten thousand steps are cumbersome in a spreadsheet. Furthermore, the analytic solution us gives more insight into the way the parameters of the carbon cycle interact to govern its behavior.
Saturday, October 17, 2015
Carbon 14: Reservoir Concentration
Our study of carbon-14, which began with Carbon-14: Origins and Reservoir, reveals that the atmosphere is exchanging carbon dioxide with a reservoir that contains over a hundred times as much carbon dioxide as the atmosphere itself. This exchange must be taking place, because it is the only means by which carbon-14 can be transported out of the atmosphere. The concentration of carbon-14 in the reservoir must be less than in the atmosphere, or else the carbon dioxide exchange would be unable to generate a net flow of carbon-14 into the reservoir.
We guessed that the reservoir was the deep ocean, which does have an adequate capacity to hold the reservoir CO2 in solution. If the deep ocean is the reservoir, its carbon-14 concentration has been measured to be 0.8 ppt, which is indeed less than the atmosphere's 1.0 ppt. Assuming the concentration of the reservoir is 0.8 ppt, we conclude that the carbon dioxide exchange rate in our natural, equilibrium atmosphere is 140 Pg/yr of CO2 (or 37 Pg/yr of carbon), while the reservoir holds 280,000 Pg of CO2 (or 77,000 Pg of carbon). Because our equilibrium atmosphere itself holds 2,400 Pg of CO2 (or 650 Pg of carbon), we see that 5.6% of the CO2 in the atmosphere enters the reservoir every year and is replaced by a like amount emerging from the reservoir. Furthermore, the reservoir holds 120 times as much CO2 as the atmosphere.
In future posts, we will find that the vast size of the reservoir, combined with the ready exchange of carbon dioxide between it and the atmosphere, imply that continuing to burn fossil fuels at the rate we are today will take thousands of years to cause a doubling in the carbon dioxide concentration of the atmosphere. Before we proceed, however, let us consider how our estimate of the size of the reservoir and the magnitude of the exchange are affected by uncertainty in the one parameter that we have guessed at: the concentration of carbon-14 in the reservoir. This concentration must be less than 1.0 ppt, and we guessed it is 0.8 ppt. But perhaps it is 0.7 ppt or 0.9 ppt. Using the equations we derived last time, we re-calculate the carbon exchange rate and the reservoir size for these concentrations.
Table: Effect of Reservoir Concentration. We have reservoir concentration of carbon-14 in ppt, CR, carbon mass exchange rate in Pg/yr, me, and reservoir carbon mass in Pg, MR. Multiply carbon masses by 44/12 to get CO2 masses.
In Arnold et al., the authors present measurements of carbon-14 concentration in various layers of the ocean, in vegetation, and in soil, relative to the carbon-14 concentration in the atmosphere. These vary from 80% to 96% of the atmospheric concentration, with the deep oceans having the lowest concentration. The concentration in our reservoir must lie somewhere in the range 0.8-1.0 ppt. If the concentration is higher than 0.8 ppt, the reservoir will be slightly smaller, but the exchange rate will be much higher. At 0.9 ppt, for example, the exchange rate will be double what it is for 0.8 ppt. We see that our estimate of the exchange rate, being based upon a reservoir concentration of 0.8 ppt, is a conservative one, while our estimate of the reservoir size is bound to be close. We can now proceed with confidence in our analysis, knowing that we are certain not to over-estimate the exchange of carbon dioxide between the atmosphere and the reservoir.
We guessed that the reservoir was the deep ocean, which does have an adequate capacity to hold the reservoir CO2 in solution. If the deep ocean is the reservoir, its carbon-14 concentration has been measured to be 0.8 ppt, which is indeed less than the atmosphere's 1.0 ppt. Assuming the concentration of the reservoir is 0.8 ppt, we conclude that the carbon dioxide exchange rate in our natural, equilibrium atmosphere is 140 Pg/yr of CO2 (or 37 Pg/yr of carbon), while the reservoir holds 280,000 Pg of CO2 (or 77,000 Pg of carbon). Because our equilibrium atmosphere itself holds 2,400 Pg of CO2 (or 650 Pg of carbon), we see that 5.6% of the CO2 in the atmosphere enters the reservoir every year and is replaced by a like amount emerging from the reservoir. Furthermore, the reservoir holds 120 times as much CO2 as the atmosphere.
In future posts, we will find that the vast size of the reservoir, combined with the ready exchange of carbon dioxide between it and the atmosphere, imply that continuing to burn fossil fuels at the rate we are today will take thousands of years to cause a doubling in the carbon dioxide concentration of the atmosphere. Before we proceed, however, let us consider how our estimate of the size of the reservoir and the magnitude of the exchange are affected by uncertainty in the one parameter that we have guessed at: the concentration of carbon-14 in the reservoir. This concentration must be less than 1.0 ppt, and we guessed it is 0.8 ppt. But perhaps it is 0.7 ppt or 0.9 ppt. Using the equations we derived last time, we re-calculate the carbon exchange rate and the reservoir size for these concentrations.
| CR (ppt) | me (Pg/yr of Carbon) | MR (Pg of Carbon) |
|---|---|---|
| 0.7 | 24 | 88,000 |
| 0.8 | 37 | 77,000 |
| 0.9 | 74 | 69,000 |
In Arnold et al., the authors present measurements of carbon-14 concentration in various layers of the ocean, in vegetation, and in soil, relative to the carbon-14 concentration in the atmosphere. These vary from 80% to 96% of the atmospheric concentration, with the deep oceans having the lowest concentration. The concentration in our reservoir must lie somewhere in the range 0.8-1.0 ppt. If the concentration is higher than 0.8 ppt, the reservoir will be slightly smaller, but the exchange rate will be much higher. At 0.9 ppt, for example, the exchange rate will be double what it is for 0.8 ppt. We see that our estimate of the exchange rate, being based upon a reservoir concentration of 0.8 ppt, is a conservative one, while our estimate of the reservoir size is bound to be close. We can now proceed with confidence in our analysis, knowing that we are certain not to over-estimate the exchange of carbon dioxide between the atmosphere and the reservoir.
Tuesday, October 13, 2015
Carbon 14: Size of the Carbon Reservoir
Carbon-14 is produced at roughly 7.5 kg/yr in the atmosphere. Its atmospheric concentration is one part per trillion (1.0 ppt). Its half-life is 5700 years. These three observations imply the existence of the carbon cycle we described in our previous post. Our graphical representation of the carbon cycle uses the quantities listed in the table below. Together, these quantities provide a complete description of the cycle. Their numerical values apply to our natural, equilibrium atmosphere, which is based upon the Earth's atmosphere at the end of the nineteenth century. So far, we have values for all but two of these quantities: the mass of carbon in the reservoir, and the mass of carbon exchanged each year between the reservoir and the atmosphere.
Table: Carbon Cycle Quantities. We have 1 Pg = one petagram = 1012 kg = 1015 g.
Another way to represent the carbon cycle is with two differential equations, as shown below, where d/dt represents the rate of change of a quantity with time, where t is time in years. Thus dCA/dt is the rate of change of the concentration of carbon-14 in the atmosphere with time, in units of ppt/yr.
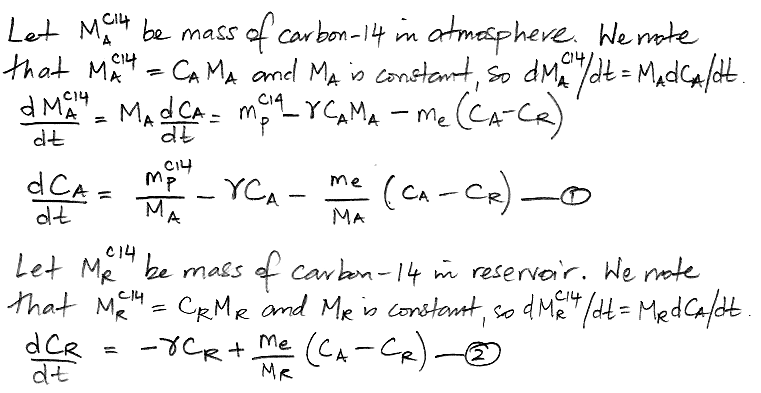
When our carbon cycle reaches equilibrium, the concentration of carbon-14 in the atmosphere and the reservoir settles to a constant value, so the d/dt terms are zero. This observation reduces our two differential equations to two simple algebraic equations, and we can solve for our two unknown quantities.
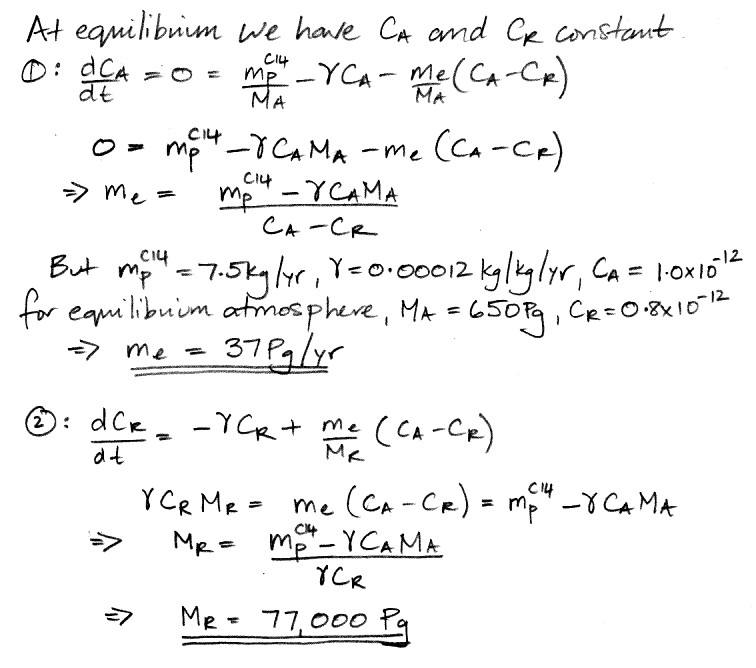
We have 37 Pg of carbon transported into the reservoir every year, including 37.0 kg of carbon-14 because the atmosphere's concentration of carbon-14 is 1.0 ppt. Another 37 Pg of carbon is emitted by the reservoir every year, including 29.6 kg of carbon-14 because the reservoir's concentration of carbon-14 is 0.8 ppt. The net flow of carbon-14 is 7.4 kg/yr into the reservoir (subtract 29.6 kg/yr from 37 kg/yr). The reservoir itself, meanwhile, contains 77,000 Pg of carbon, of which 62,000 kg is carbon-14. The reservoir's carbon-14 decays at 7.4 kg/yr (multiply 62,000 kg by 0.0012 kg/kg/yr ). As is required by the state of equilibrium, the net flow of carbon-14 into the reservoir each year is equal to the amount of carbon-14 that decays in the reservoir each year. We also have 0.1 kg of carbon-14 decaying in the atmosphere each year, so the total mass of carbon-14 that decays each year is 7.5 kg, which is equal to the amount that cosmic rays create, which is also required by the state of equilibrium.
Although our quantities deal only with masses of carbon, we note that all exchanges of carbon between the atmosphere and the reservoir take place in the form of exchanges of CO2. In particular, all carbon-14 in the atmosphere is bound up in CO2. We assumed earlier in our argument that the residence time of carbon carbon-14 in the atmosphere was much longer than the two months it takes for newly-created carbon-14 to react with oxygen to form CO2. We can now check the validity of this assumption: we have 650 Pg of carbon in the atmosphere, and 37 Pg of carbon flowing from the atmosphere into the reservoir each year. The residence time of a carbon-14 atom in the atmosphere is eighteen years (divide 650 Pg by 37 Pg/yr), which is much longer than two months, so our assumption turns out to be correct.
We conclude that our natural, equilibrium atmosphere exchanges 37 Pg of carbon each year with a reservoir that contains 77,000 Pg of carbon. Furthermore, because all carbon in the atmosphere is in the form of CO2, and all exchanges of carbon with the reservoir are in the form of CO2, the atmosphere exchanges 140 Pg of CO2 with the reservoir every year, and the reservoir itself contains 280,000 Pg CO2 (multiply by carbon mass by the molecular weight of CO2 and divide by the atomic weight of carbon). Meanwhile, the 650 Pg of atmospheric carbon is contained in 2,400 Pg of atmospheric CO2. That is to say: the carbon reservoir is a CO2 reservoir, and it contains more than a hundred times as much CO2 as the atmosphere.
| Symbol | Quantity | Value |
|---|---|---|
| mpC14 | production rate of carbon-14 in atmosphere | 7.5 kg/yr |
| γ | decay rate of carbon-14 | 0.00012 kg/kg/yr |
| MA | mass of carbon in the atmosphere | 650 Pg |
| CA | concentration of carbon-14 in atmosphere | 1.0 ppt at equilibrium |
| MR | mass of carbon in the reservoir | unknown, Pg |
| me | exchange rate of CO2 between atmosphere and reservoir | unknown, Pg/yr |
| CR | concentration of carbon-14 in reservoir | 0.8 ppt at equilibrium |
Another way to represent the carbon cycle is with two differential equations, as shown below, where d/dt represents the rate of change of a quantity with time, where t is time in years. Thus dCA/dt is the rate of change of the concentration of carbon-14 in the atmosphere with time, in units of ppt/yr.
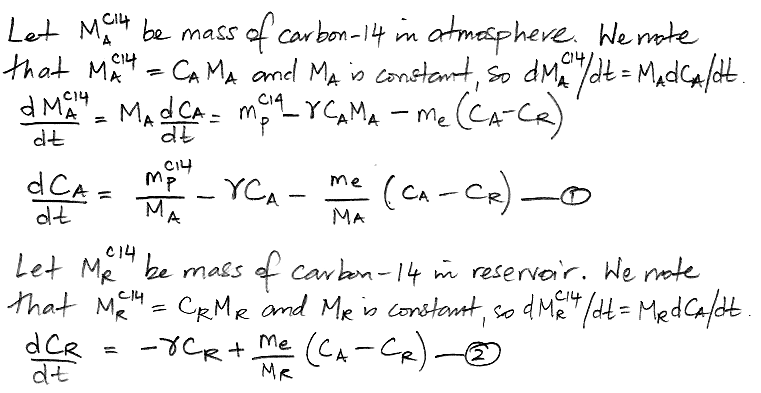
When our carbon cycle reaches equilibrium, the concentration of carbon-14 in the atmosphere and the reservoir settles to a constant value, so the d/dt terms are zero. This observation reduces our two differential equations to two simple algebraic equations, and we can solve for our two unknown quantities.
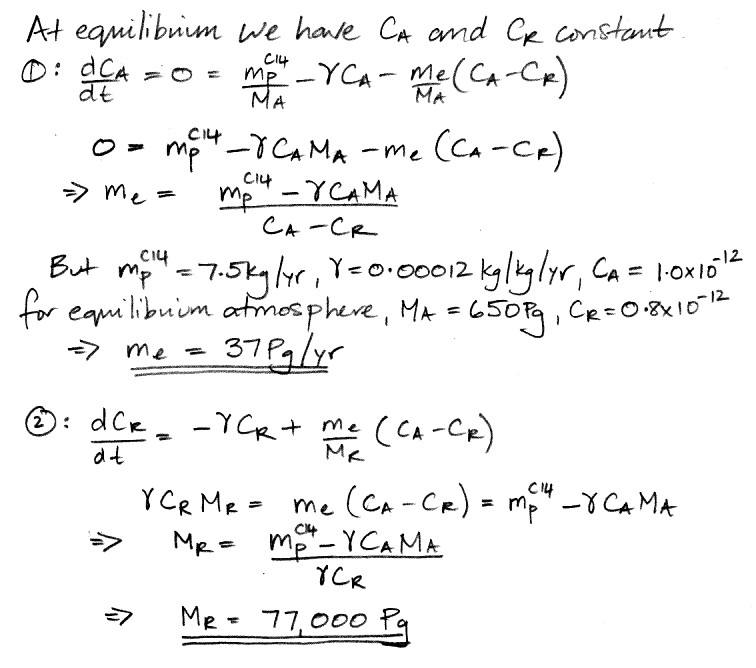
We have 37 Pg of carbon transported into the reservoir every year, including 37.0 kg of carbon-14 because the atmosphere's concentration of carbon-14 is 1.0 ppt. Another 37 Pg of carbon is emitted by the reservoir every year, including 29.6 kg of carbon-14 because the reservoir's concentration of carbon-14 is 0.8 ppt. The net flow of carbon-14 is 7.4 kg/yr into the reservoir (subtract 29.6 kg/yr from 37 kg/yr). The reservoir itself, meanwhile, contains 77,000 Pg of carbon, of which 62,000 kg is carbon-14. The reservoir's carbon-14 decays at 7.4 kg/yr (multiply 62,000 kg by 0.0012 kg/kg/yr ). As is required by the state of equilibrium, the net flow of carbon-14 into the reservoir each year is equal to the amount of carbon-14 that decays in the reservoir each year. We also have 0.1 kg of carbon-14 decaying in the atmosphere each year, so the total mass of carbon-14 that decays each year is 7.5 kg, which is equal to the amount that cosmic rays create, which is also required by the state of equilibrium.
Although our quantities deal only with masses of carbon, we note that all exchanges of carbon between the atmosphere and the reservoir take place in the form of exchanges of CO2. In particular, all carbon-14 in the atmosphere is bound up in CO2. We assumed earlier in our argument that the residence time of carbon carbon-14 in the atmosphere was much longer than the two months it takes for newly-created carbon-14 to react with oxygen to form CO2. We can now check the validity of this assumption: we have 650 Pg of carbon in the atmosphere, and 37 Pg of carbon flowing from the atmosphere into the reservoir each year. The residence time of a carbon-14 atom in the atmosphere is eighteen years (divide 650 Pg by 37 Pg/yr), which is much longer than two months, so our assumption turns out to be correct.
We conclude that our natural, equilibrium atmosphere exchanges 37 Pg of carbon each year with a reservoir that contains 77,000 Pg of carbon. Furthermore, because all carbon in the atmosphere is in the form of CO2, and all exchanges of carbon with the reservoir are in the form of CO2, the atmosphere exchanges 140 Pg of CO2 with the reservoir every year, and the reservoir itself contains 280,000 Pg CO2 (multiply by carbon mass by the molecular weight of CO2 and divide by the atomic weight of carbon). Meanwhile, the 650 Pg of atmospheric carbon is contained in 2,400 Pg of atmospheric CO2. That is to say: the carbon reservoir is a CO2 reservoir, and it contains more than a hundred times as much CO2 as the atmosphere.
Friday, October 9, 2015
Carbon-14: The Carbon Cycle
When a carbon-14 atom is created in the atmosphere by a cosmic ray, it quickly combines with oxygen to form carbon monoxide (CO). In a couple of months, this carbon monoxide combines with more oxygen to form radioactive carbon dioxide (CO2). As we showed previously, almost all carbon-14 created in the atmosphere ends up in a reservoir outside the atmosphere. But how long does the average carbon-14 atom spend in the atmosphere before it leaves? Our equilibrium atmosphere contains 650 kg of carbon-14, while 7.5 kg are created by cosmic rays every year. Almost one century's worth of carbon-14 production is stored in the atmosphere. It is most likely, therefore, that the averge carbon-14 atom spends several years in the atmosphere before it passes into the reservoir. Let us assume, for now, that the residence time of carbon-14 in the atmosphere is much longer than the two months it takes for carbon-14 to be bound up into a CO2 molecule. We will come back and check the validity of this assumption later. For now, we assume that all carbon-14 in the atmosphere is bound up in radioactive CO2.
The composition of the atmosphere is such that over 99.5% of its carbon is in the form of CO2. When we observe that one in a trillion carbon atoms is carbon-14, this is equivalent to saying that one in a trillion CO2 molecules is radioactive CO2. But radioactive CO2 is chemically identical to normal CO2. The extra two neutrons in its carbon nucleus have no effect upon its interactions with other molecules. When one molecule of radioactive CO2 leaves an atmosphere that contains 1 ppt (one part per trillion) of carbon-14, it does so in the company of one trillion normal CO2 molecules. When one carbon-14 atom leaves the atmosphere, it does so with one trillion other carbon atoms. The reservoir of carbon-14 that must exist outside the atmosphere must also be a much larger reservoir of normal carbon. The concentration of carbon-14 in this reservoir cannot be greater than in the atmosphere, because the atmosphere is where the carbon-14 is created. We already calculated that the reservoir contains 62 Mg of carbon-14, so it must also contain at least 62,000 Pg (sixty-two thousand Petagrams) of normal carbon (divide the mass of carbon-14 by the maximum possible concentration of carbon-14 in the reservoir). The reservoir contains one hundred times as much carbon as our equilibrium atmosphere.
In order for carbon-14 to leave the atmosphere, it must be carried by radioactive carbon dioxide, which in turn means that there must be a trillion times as much normal carbon dioxide leaving the atmosphere. But our equilibirum atmosphere is, by assumption, in in equilibrium. Its carbon dioxide content, and therefore its carbon content, is constant. If me kilograms of carbon leave the atmosphere every year and enter the reservoir, we must have the same me kilograms of carbon leaving the reservoir and entering the atmosphere every year. Thus the carbon content of the reservoir remains constant as well.
If the carbon-14 concentration of the reservoir were the same as the atmosphere's, we would have the same amount of carbon-14 leaving the atmosphere as returning, because the amount of normal carbon leaving is the same as the amount returning. Therefore, the concentration of carbon-14 in the reservoir must be lower than in the atmosphere. Let the concentration in the atmosphere be CA and in the reservoir be CR. The net flow of carbon-14 out of the atmosphere will be me(CA−CR), which we already calculated to be 7.4 kg/yr.
It remains for us to estimate the equilibrium concentration of carbon-14 in our carbon reservoir. It is well known that carbon is stored in vegetation and in the oceans. One kilogram of water at 14°C will hold around 0.5 g of carbon in the form of dissolved CO2. Given that the mass of the oean is roughly 1.4×1021 kg, the oceans have have the potential to store up to 700,000 Pg of carbon. The Earth's biomass, meanwhile, appears to contain only 2,000 Pg of carbon. So we will assume that the majority of the Earth's carbon reservoir is in the oceans. The concentration of carbon-14 in the deep oceans was measured by Bien et al. to be around 80% of the concentration in the atmosphere. So we will assume that the equilibrium concentration of carbon-14 in the Earth's carbon-14 reservoir is 0.8 ppt.
The diagram below illustrates what we have concluded so far about the exchange of carbon between the atmosphere and the reservoir. The masses of carbon in the atmosphere and the reservoir are MA and MR respectively. The decay rate of carbon-14 is γ.
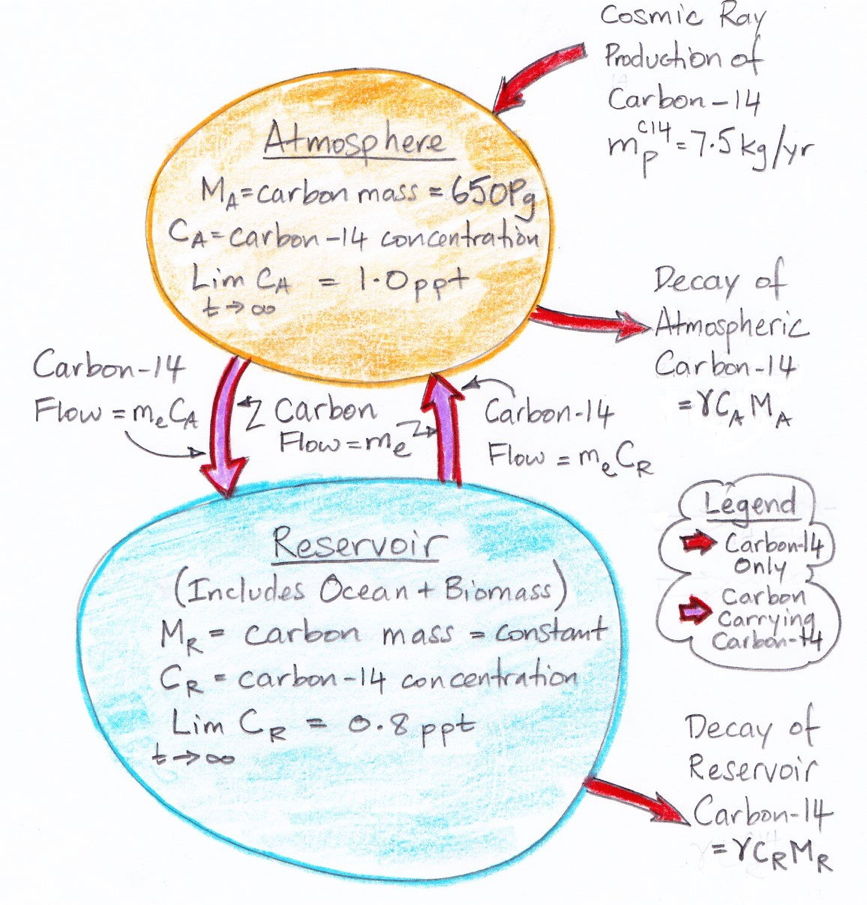
The diagram assumes that the carbon exchange between the atmosphere and the reservoir has already reached equilibrium. But it does not assume that the carbon-14 concentration has reached equilibrium. We are going to obtain an analytic solution for the evolution of carbon-14 concentration from a starting point of no carbon-14 at all. So instead of pre-supposing that we have already reached carbon-14 equilibrium, the diagram states that, given infinite time, the carbon-14 concentration in the atmosphere and reservoir will eventually reach equilibrium at 1.0 and 0.8 ppt respectively.
What is expressed in the diagram we can write down in two differential equations with some boundary conditions. The two equations contain two unknown constants: the carbon exchange rate, me, and the size of the carbon reservoir, MR. In our next post, we will use these two differential equations to deduce the values of me and MR.
The composition of the atmosphere is such that over 99.5% of its carbon is in the form of CO2. When we observe that one in a trillion carbon atoms is carbon-14, this is equivalent to saying that one in a trillion CO2 molecules is radioactive CO2. But radioactive CO2 is chemically identical to normal CO2. The extra two neutrons in its carbon nucleus have no effect upon its interactions with other molecules. When one molecule of radioactive CO2 leaves an atmosphere that contains 1 ppt (one part per trillion) of carbon-14, it does so in the company of one trillion normal CO2 molecules. When one carbon-14 atom leaves the atmosphere, it does so with one trillion other carbon atoms. The reservoir of carbon-14 that must exist outside the atmosphere must also be a much larger reservoir of normal carbon. The concentration of carbon-14 in this reservoir cannot be greater than in the atmosphere, because the atmosphere is where the carbon-14 is created. We already calculated that the reservoir contains 62 Mg of carbon-14, so it must also contain at least 62,000 Pg (sixty-two thousand Petagrams) of normal carbon (divide the mass of carbon-14 by the maximum possible concentration of carbon-14 in the reservoir). The reservoir contains one hundred times as much carbon as our equilibrium atmosphere.
In order for carbon-14 to leave the atmosphere, it must be carried by radioactive carbon dioxide, which in turn means that there must be a trillion times as much normal carbon dioxide leaving the atmosphere. But our equilibirum atmosphere is, by assumption, in in equilibrium. Its carbon dioxide content, and therefore its carbon content, is constant. If me kilograms of carbon leave the atmosphere every year and enter the reservoir, we must have the same me kilograms of carbon leaving the reservoir and entering the atmosphere every year. Thus the carbon content of the reservoir remains constant as well.
If the carbon-14 concentration of the reservoir were the same as the atmosphere's, we would have the same amount of carbon-14 leaving the atmosphere as returning, because the amount of normal carbon leaving is the same as the amount returning. Therefore, the concentration of carbon-14 in the reservoir must be lower than in the atmosphere. Let the concentration in the atmosphere be CA and in the reservoir be CR. The net flow of carbon-14 out of the atmosphere will be me(CA−CR), which we already calculated to be 7.4 kg/yr.
It remains for us to estimate the equilibrium concentration of carbon-14 in our carbon reservoir. It is well known that carbon is stored in vegetation and in the oceans. One kilogram of water at 14°C will hold around 0.5 g of carbon in the form of dissolved CO2. Given that the mass of the oean is roughly 1.4×1021 kg, the oceans have have the potential to store up to 700,000 Pg of carbon. The Earth's biomass, meanwhile, appears to contain only 2,000 Pg of carbon. So we will assume that the majority of the Earth's carbon reservoir is in the oceans. The concentration of carbon-14 in the deep oceans was measured by Bien et al. to be around 80% of the concentration in the atmosphere. So we will assume that the equilibrium concentration of carbon-14 in the Earth's carbon-14 reservoir is 0.8 ppt.
The diagram below illustrates what we have concluded so far about the exchange of carbon between the atmosphere and the reservoir. The masses of carbon in the atmosphere and the reservoir are MA and MR respectively. The decay rate of carbon-14 is γ.

The diagram assumes that the carbon exchange between the atmosphere and the reservoir has already reached equilibrium. But it does not assume that the carbon-14 concentration has reached equilibrium. We are going to obtain an analytic solution for the evolution of carbon-14 concentration from a starting point of no carbon-14 at all. So instead of pre-supposing that we have already reached carbon-14 equilibrium, the diagram states that, given infinite time, the carbon-14 concentration in the atmosphere and reservoir will eventually reach equilibrium at 1.0 and 0.8 ppt respectively.
What is expressed in the diagram we can write down in two differential equations with some boundary conditions. The two equations contain two unknown constants: the carbon exchange rate, me, and the size of the carbon reservoir, MR. In our next post, we will use these two differential equations to deduce the values of me and MR.
Subscribe to:
Posts (Atom)
