In our previous post, we concluded that air above the desert cools down by 10°C in the first hour after sunset because cold air descends slowly from above as the day's convection cycle comes to a stop. This explanation is not one of the several you will find on the web if you search for "Why does the desert get so cold at night?" These other explanations talk about dry air allowing heat to radiate away into space. But our calculations in Day and Night showed that the rate at which the Earth and its atmosphere radiate heat is barely adequate to cool the air by half a degree in ten hours, let alone ten degrees in one hour.
One of our readers points us to another night-time cooling phenomenon called "night inversion". According to this description, the air immediately above a forest can be 10°C cooler at night than the air 100 m up. In our explanation of the desert cooling, the cold air above the desert was still warmer than the air higher up, but in this case, the air above the forest is actually colder than the air higher up. We will conclude our Surface Cooling series by offering an explanation for nigh inversion also.
The first 100 m of the atmosphere has heat capacity 100 kJ/K/m2. The forest is a good black body, so it will radiate of order 100 W/m2 directly into space through a clear night sky. A leaf, being roughly 1 mm thick, and consisting mostly of water, has heat capacity roughly 4 kJ/K/m2. When it radiates 100 W/m2 it will tend to cool by more than 1°C every minute. It is the heat capacity of the air around it that will stop the leaf from freezing.
The forest leaves will set up a convection cycle in which air is cooled by the upper leaves, which are the ones radiating into space, and warmed by the surface of the Earth below. The air immediately above the forest will be sucked into this cycle, and the air immediately above that also, so that the very cold air of the tree-tops mixes slowly with the air ten to a hundred meters up, creating a layer of air that is colder and more dense than the air above. The convection cycle transports roughly 100 W/m2. Suppose that the mixing we describe causes 30 W/m2 to be removed from the heat capacity of the first 100 m of air. In that case, the average temperature of the first 100 m will drop by 5°C in six hours.
So we see that radiation by leaves held ten or twenty meters above the ground can cause the first hundred meters of the atmosphere to cool by several degrees compared to the air above, and so create a static, cold layer of air above the forest. If there is any wind, of course, the leaves will no longer need their convection cycle to keep them warm: the wind will warm them, and blow away any cold air as well. The night must be still for such inversion to take place, and air is more often still in a bowl or valley.
Our Surface Cooling posts have introduced us to the heat capacity of the atmosphere, and shown us that traditional explanations for cooling and warming may be unreliable. But we have no proof that it is an exchange of warm air for cold air that causes the sudden drop in temperature at sunset in the desert. Nor do we have any proof that a cold convection cycle in a forest causes night inversion. Both explanations are merely hypotheses. Any help devising experiments to test either hypothesis would be much appreciated. Our ideas so far, which involve helium balloons and battery-powered thermometers, appear impractical, not to mention expensive.
Thursday, December 30, 2010
Tuesday, December 21, 2010
Surface Cooling, Part III
UPDATE: The original version of this post included an argument by Second Law of Thermodynamics that, although correct, did not point out the actual physical mechanism by which desert air cools at sunset. I cut out this argument and added a description of the physical mechanism as suggested by my father.
The air above the desert cools by 20°C at night. But the heat capacity of the air above the desert is so great that it is impossible for it to cool so quickly by radiation into space or by conduction to the ground. We ended our previous post with the suggestion that the drop in temperature over the desert at night is caused not by the cooling of air, but by the replacement of warm air by cold air.
In Biggles Flies South, the author tells us that flying over the desert during the day is exhausting and uncomfortable because the air is so "bumpy". The best time to fly is the early morning, when the air is still and there is daylight to see by. Our understanding of atmospheric convection suggests that the air above the desert will be a succession of convection cycles, something like the drawing below, where small features of the surface end up dictating the boundaries of the cycles, and the cycles are angled sideways by a prevailing wind.
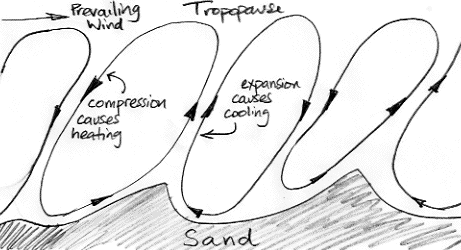
All this convection is caused by the sun heating the desert sand until it warms the air and causes the air to rise. But when the sun goes down, the sand cools off quickly. The circulation will eventually come to a stop, but it's momentum will keep it going for a while. When it is near to stopping, air is descending slowly from above, and comes to a stop. The sand is no longer hot, and no longer warms the air.
When the sun goes down over the desert, the day-time convection of the atmosphere slows to a halt. The slowing cycle brings cold air down from above. This cold air is not warmed by the hot sand as it would be during the day. The temperature drops by ten or twenty degrees in an hour. For the rest of the night, the air is still and cools slowly by radiating into space. Perhaps the temperature will drop by another one or two degrees by dawn.
The air above the desert cools by 20°C at night. But the heat capacity of the air above the desert is so great that it is impossible for it to cool so quickly by radiation into space or by conduction to the ground. We ended our previous post with the suggestion that the drop in temperature over the desert at night is caused not by the cooling of air, but by the replacement of warm air by cold air.
In Biggles Flies South, the author tells us that flying over the desert during the day is exhausting and uncomfortable because the air is so "bumpy". The best time to fly is the early morning, when the air is still and there is daylight to see by. Our understanding of atmospheric convection suggests that the air above the desert will be a succession of convection cycles, something like the drawing below, where small features of the surface end up dictating the boundaries of the cycles, and the cycles are angled sideways by a prevailing wind.

All this convection is caused by the sun heating the desert sand until it warms the air and causes the air to rise. But when the sun goes down, the sand cools off quickly. The circulation will eventually come to a stop, but it's momentum will keep it going for a while. When it is near to stopping, air is descending slowly from above, and comes to a stop. The sand is no longer hot, and no longer warms the air.
When the sun goes down over the desert, the day-time convection of the atmosphere slows to a halt. The slowing cycle brings cold air down from above. This cold air is not warmed by the hot sand as it would be during the day. The temperature drops by ten or twenty degrees in an hour. For the rest of the night, the air is still and cools slowly by radiating into space. Perhaps the temperature will drop by another one or two degrees by dawn.
Wednesday, December 15, 2010
Surface Cooling, Part II
In our Surface Cooling, Part I, we saw that the air above the ocean cools by less than 1°C at night. The air above the desert in Arizona, however, cools by 20°C at night. In Night and Day we saw that the heat radiated into space by the Earth is barely sufficient to cool the atmosphere by 1°C at night, let alone 20°C, so we are left wondering how the air above the desert can cool down so fast.
The table below presents the thermal properties of some common surface materials. We will make use of this table in future posts. Values for composite materials like wet soil are approximate. We picked values that are representative from resources like this, this, and this. Today we will use only the properties of dry sand. In the first column we have the thermal conductivity in Watt per meter per Kelvin (W/mK = W/m°C). A layer of material with thermal conductivity α, thickness d, temperature Tb at the bottom and Tt at the top, will conduct α(Tb−Tt)/d for each square meter of its surface area. A 10-cm thick layer of dry sand that is 20°C cooler on top than bottom will conduct 0.20 W/mK × 20 °C / 0.1 m = 40 W/m2.
Our SC1 program simulates the cooling of the surface of the Earth at night. You can download it and run it yourself, by following the instructions in the code. The program works by dividing the surface material into thin layers and calculating the temperature of each layer in a sequence of small time steps. We assume the material is at a uniform temperature when it begins to cool, and that the heat loss from the upper surface is a constant 200 W/2. In earlier versions of the code, we calculated the surface loss as a combination of radiation into space and convection with the surface air, but our results were pretty much the same, so we reverted to the assumption of constant loss to keep things simple.
The following graph shows what our simulation program tells us happens to dry sand at various depths in millimeters when it starts to cool from the surface at 200 W/m2. We see the surface cools by 13°C in 1000s while the sand 40 mm down cools by roughly 0.1°C.
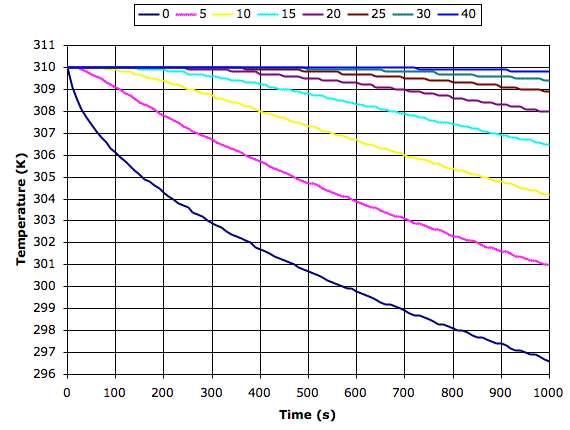
Materials with greater conductivity cool more slowly because heat rises from below to keep the surface warm. If we apply our simulation program to sandstone or asphalt, we find the surface cools down ten times more slowly than the surface of dry sand. So it is above dry sand or soil that we expect to see the greatest drop in surface temperature at night.
Our calculations show that a sandy surface can cool by 20°C at night. They show that one meter down, the heat of the day will hardly affect the temperature of the sand. But they still don't explain why the temperature above the desert sand cools by 20°C at night. The surface of the sand cools down because it loses heat to the air and to outer space. If anything, the cooling sand warms the air. We already know that the heat radiated by the air itself is not sufficient to cause such cooling. Indeed, our calculations show that it is impossible for air above the desert to cool by 20°C at night. And yet we know that a thermometer 2 m above the surface of the desert can register a drop of 20°C.
We conclude that the air above the sand at night cannot be the same air above the sand during the day, and indeed this conclusion leads us to a most satisfactory explanation for cold desert nights.
The table below presents the thermal properties of some common surface materials. We will make use of this table in future posts. Values for composite materials like wet soil are approximate. We picked values that are representative from resources like this, this, and this. Today we will use only the properties of dry sand. In the first column we have the thermal conductivity in Watt per meter per Kelvin (W/mK = W/m°C). A layer of material with thermal conductivity α, thickness d, temperature Tb at the bottom and Tt at the top, will conduct α(Tb−Tt)/d for each square meter of its surface area. A 10-cm thick layer of dry sand that is 20°C cooler on top than bottom will conduct 0.20 W/mK × 20 °C / 0.1 m = 40 W/m2.
Conductivity Density CapacityThe second column gives the density in kilogram per cubic meter (kg/m3). A 10-cm layer of dry sand has mass 0.1 m × 1700 kg = 170 kg/m2. The third column gives the specific heat capacity in Joule per kilogram per kelvin ( J/kgK = J/kg°C). A layer of material with specific heat capacity C, density ρ, and thickness d will require Cρd Joules of heat per square meter of surface area to raise its temperature by 1°C. A 10-cm thick layer of dry sand requires 800 J/kgK × 1700 kg × 0.1 m = 136 kJ/m2 to warm up by 1°C. Alternatively, we must remove 136 kJ/m2 to cool it by 1°C. If this layer loses loses 80 W/m2, it will take half an hour to cool down by 1°C.
Material (W/mK) (kg/m^3) (J/kgK)
Air 0.024 1.2 1000
Asphalt 0.75 1300 920
Copper 390 8900 420
Ice 2.2 910 2000
Mercury 8.7 14000 140
Sand, Dry 0.20 1600 830
Sand, Wet 4.0 2000 2500
Sandstone 1.7 2500 800
Soil, Dry 0.4 1300 1400
Soil, Wet 4.0 1500 2500
Snow, Light 0.10 100 420
Steel 43 7800 460
Water 0.58 1000 4200
Wood, Oak 0.17 770 1700
Our SC1 program simulates the cooling of the surface of the Earth at night. You can download it and run it yourself, by following the instructions in the code. The program works by dividing the surface material into thin layers and calculating the temperature of each layer in a sequence of small time steps. We assume the material is at a uniform temperature when it begins to cool, and that the heat loss from the upper surface is a constant 200 W/2. In earlier versions of the code, we calculated the surface loss as a combination of radiation into space and convection with the surface air, but our results were pretty much the same, so we reverted to the assumption of constant loss to keep things simple.
The following graph shows what our simulation program tells us happens to dry sand at various depths in millimeters when it starts to cool from the surface at 200 W/m2. We see the surface cools by 13°C in 1000s while the sand 40 mm down cools by roughly 0.1°C.

Materials with greater conductivity cool more slowly because heat rises from below to keep the surface warm. If we apply our simulation program to sandstone or asphalt, we find the surface cools down ten times more slowly than the surface of dry sand. So it is above dry sand or soil that we expect to see the greatest drop in surface temperature at night.
Our calculations show that a sandy surface can cool by 20°C at night. They show that one meter down, the heat of the day will hardly affect the temperature of the sand. But they still don't explain why the temperature above the desert sand cools by 20°C at night. The surface of the sand cools down because it loses heat to the air and to outer space. If anything, the cooling sand warms the air. We already know that the heat radiated by the air itself is not sufficient to cause such cooling. Indeed, our calculations show that it is impossible for air above the desert to cool by 20°C at night. And yet we know that a thermometer 2 m above the surface of the desert can register a drop of 20°C.
We conclude that the air above the sand at night cannot be the same air above the sand during the day, and indeed this conclusion leads us to a most satisfactory explanation for cold desert nights.
Wednesday, December 8, 2010
Surface Cooling, Part I
In Day and Night we found that the heat capacity of the atmosphere keeps the Earth warm at night. There are ten tons of air above every square meter of the Earth, and this ten tons has heat capacity 10 MJ/°C. When the atmosphere radiates 200 W/m2 into space, which is typical of a clear sky, its average temperature drops by less than 1°C in twelve hours.
The heat capacity of water, meanwhile, keeps a pond warm at night. In a 1-m deep pond, there is a ton of water beneath every square meter of surface, and this ton has heat capacity 4 MJ/°C. If the water surface radiates 80 W/m2 into space, which is typical when the sky is clear, this radiation will cool the pond by less than 1°C in twelve hours. The water surface will, of course, be losing more heat by atmospheric convection and by evaporation. But in the ocean, where the top ten meters of water are well-mixed by waves, even a surface loss of 800 W/m2 will cool the water by less than 1°C at night.
Here is a twenty-day recording of air and water temperature from an ocean buoy, which we obtained from the National Data Buoy Center. The data is here.
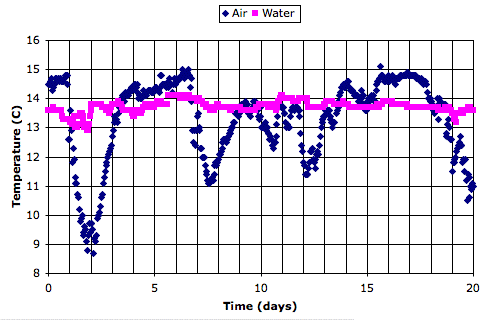
We see that the air temperature varies by 5°C from one week to the next, but by less than 1°C from day to night. The water itself, meanwhile, is hardly affected by the weekly variations, and not at all by the daily variations.
Why, then, does the temperature in Arizona drop by 20°C at night? The surface of Arizona is sand and rocks. These solid, opaque materials transport heat within themselves by conduction alone. During the day, their surfaces get hot. During the night, they cool down. In our next post, we will present the thermal properties of some common surface materials, along with a computer program to calculate how fast these surface materials will cool at night. We will find out whether the thermal properties of sand can explain why the desert is hot in the day and cold at night.
The heat capacity of water, meanwhile, keeps a pond warm at night. In a 1-m deep pond, there is a ton of water beneath every square meter of surface, and this ton has heat capacity 4 MJ/°C. If the water surface radiates 80 W/m2 into space, which is typical when the sky is clear, this radiation will cool the pond by less than 1°C in twelve hours. The water surface will, of course, be losing more heat by atmospheric convection and by evaporation. But in the ocean, where the top ten meters of water are well-mixed by waves, even a surface loss of 800 W/m2 will cool the water by less than 1°C at night.
Here is a twenty-day recording of air and water temperature from an ocean buoy, which we obtained from the National Data Buoy Center. The data is here.

We see that the air temperature varies by 5°C from one week to the next, but by less than 1°C from day to night. The water itself, meanwhile, is hardly affected by the weekly variations, and not at all by the daily variations.
Why, then, does the temperature in Arizona drop by 20°C at night? The surface of Arizona is sand and rocks. These solid, opaque materials transport heat within themselves by conduction alone. During the day, their surfaces get hot. During the night, they cool down. In our next post, we will present the thermal properties of some common surface materials, along with a computer program to calculate how fast these surface materials will cool at night. We will find out whether the thermal properties of sand can explain why the desert is hot in the day and cold at night.
Wednesday, December 1, 2010
Day and Night
In a previous post, we considered the dramatic change in the temperature of the moon as it revolves around the Earth. In the middle of its night, the moon cools to −190 °C. In the middle of its day, it warms to 100 °C. I was in Phoenix, Arizona last week. The sky was clear all day and all night, and the air was dry. In the middle of the night, the temperature dropped to 0°C. In the middle of the day, it rose to 20°C. The day-night variation on the moon is 290°C, but on the Earth it is only 20°C.
The moon's days are one month long. At night, the surface rocks have time to cool down, losing all the heat they gained during the day. They get so cold they draw heat out of the moon's interior, and this flow of heat from the depths of the moon is what stops the moon's surface from dropping below −190°C. During the day, the rocks heat up until they start to radiate almost as much heat as is arriving from the Sun. But some heat flows into the depths of the moon to make up for the heat drawn out during the previous night.
The moon has no atmosphere, so the only thing stopping it from cooling down to absolute zero at night is the heat capacity and thermal conductivity of its surface rocks. On Earth, we have the heat capacity of the atmosphere to keep the surface warm during the night. Above each square meter of the Earth's surface is 10,000 kg of air (see Atmospheric Weight). The heat capacity of dry air is is roughly 1 kJ/K/kg. So the air above each square meter of the Earth has heat capacity 10 MJ. The Earth and its atmosphere radiate something like 250 W/m2 into space. Suppose this 250 W/m2 were extracted uniformly from the entire column of air above each square meter of the surface. It would take 10 MJ ÷ 250 W = 10 hrs to cool the air by 1°C.
We see that the heat capacity of the atmosphere is significant in reducing the temperature changes caused by the setting of the sun or the formation of thick clouds. Indeed, the temperature changes we observe from day to night on Earth are more than ten times greater than our simple heat capacity calculation suggests. Perhaps if we consider the individual 3-km layers of the atmosphere, we will come up with a different answer.
As day turns to night, the Sun no longer warms the Earth, but the Earth and its atmosphere continue to radiate heat into space. The following table gives the escaping power in Watts per square meter from each 3-km layer of the Earth's atmosphere up to the tropopause, as calculated by our TEP2 program under conditions we describe here.
Let us ignore the heat passing up through the atmosphere by radiation and convection, and assume that the Earth's surface starts to lose 80 W/m2 when the sun sets. Suppose the surface itself is water 1 m deep. The heat capacity of water is roughly 4 kJ/K/kg and its density is 1,000 kg/m3. Beneath each square meter is fluid with heat capacity 4 MJ/K. This water will cool by only 1 °C in 10 hrs.
The 0-km layer radiates 46 W/m2 directly into space. The mass of air in this first 3-km layer is a little less than 3,000 kg, with heat capacity roughly 3 MJ/K. At a loss of 46 W/m2, this layer will cool down by only 0.5°C in ten hours.
The changes in temperature we observe at the surface of the Earth from day to night are much greater than we would expect from a consideration of the heat capacity of the atmosphere and total escaping power alone. What is going on when the sun sets, that makes the Earth's surface cool down so fast? We will hope to answer this question in our next post.
The moon's days are one month long. At night, the surface rocks have time to cool down, losing all the heat they gained during the day. They get so cold they draw heat out of the moon's interior, and this flow of heat from the depths of the moon is what stops the moon's surface from dropping below −190°C. During the day, the rocks heat up until they start to radiate almost as much heat as is arriving from the Sun. But some heat flows into the depths of the moon to make up for the heat drawn out during the previous night.
The moon has no atmosphere, so the only thing stopping it from cooling down to absolute zero at night is the heat capacity and thermal conductivity of its surface rocks. On Earth, we have the heat capacity of the atmosphere to keep the surface warm during the night. Above each square meter of the Earth's surface is 10,000 kg of air (see Atmospheric Weight). The heat capacity of dry air is is roughly 1 kJ/K/kg. So the air above each square meter of the Earth has heat capacity 10 MJ. The Earth and its atmosphere radiate something like 250 W/m2 into space. Suppose this 250 W/m2 were extracted uniformly from the entire column of air above each square meter of the surface. It would take 10 MJ ÷ 250 W = 10 hrs to cool the air by 1°C.
We see that the heat capacity of the atmosphere is significant in reducing the temperature changes caused by the setting of the sun or the formation of thick clouds. Indeed, the temperature changes we observe from day to night on Earth are more than ten times greater than our simple heat capacity calculation suggests. Perhaps if we consider the individual 3-km layers of the atmosphere, we will come up with a different answer.
As day turns to night, the Sun no longer warms the Earth, but the Earth and its atmosphere continue to radiate heat into space. The following table gives the escaping power in Watts per square meter from each 3-km layer of the Earth's atmosphere up to the tropopause, as calculated by our TEP2 program under conditions we describe here.
--------------------------------------------------The surface of the Earth radiates 390 W/m2. Of this, 80 W/m2 escapes directly into space. The rest of it is absorbed by the atmosphere. But the atmosphere radiates heat towards the surface also. The 0-km layer (the first 3 km of the atmosphere) radiates 260 W/m2 upwards and downwards. We may have thought only of the upward component in the past, but the downward component exists also, and is equal to the upward component.
Name Temp BB Layer Escaping
--------------------------------------------------
Surface 290.0 401.1 388.8 80.0
0-km 280.0 348.5 262.6 46.1
3-km 270.0 301.3 184.8 39.7
6-km 250.0 221.5 111.5 44.6
9-km 230.0 158.7 50.7 26.4
12-km 220.0 132.8 22.2 10.1
15-km 220.0 132.8 14.4 5.5
--------------------------------------------------
Total: 252.5
--------------------------------------------------
Let us ignore the heat passing up through the atmosphere by radiation and convection, and assume that the Earth's surface starts to lose 80 W/m2 when the sun sets. Suppose the surface itself is water 1 m deep. The heat capacity of water is roughly 4 kJ/K/kg and its density is 1,000 kg/m3. Beneath each square meter is fluid with heat capacity 4 MJ/K. This water will cool by only 1 °C in 10 hrs.
The 0-km layer radiates 46 W/m2 directly into space. The mass of air in this first 3-km layer is a little less than 3,000 kg, with heat capacity roughly 3 MJ/K. At a loss of 46 W/m2, this layer will cool down by only 0.5°C in ten hours.
The changes in temperature we observe at the surface of the Earth from day to night are much greater than we would expect from a consideration of the heat capacity of the atmosphere and total escaping power alone. What is going on when the sun sets, that makes the Earth's surface cool down so fast? We will hope to answer this question in our next post.
Subscribe to:
Comments (Atom)
